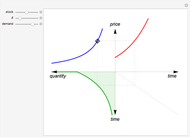
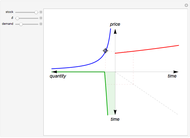
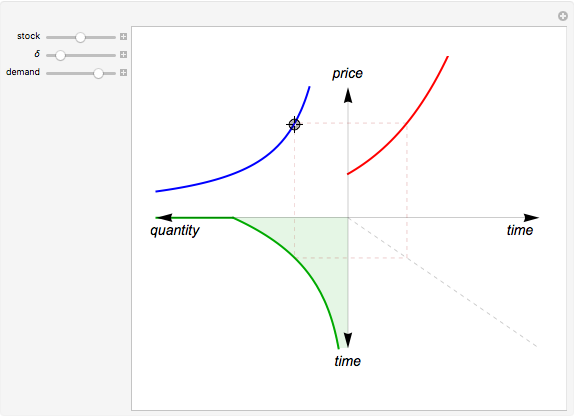
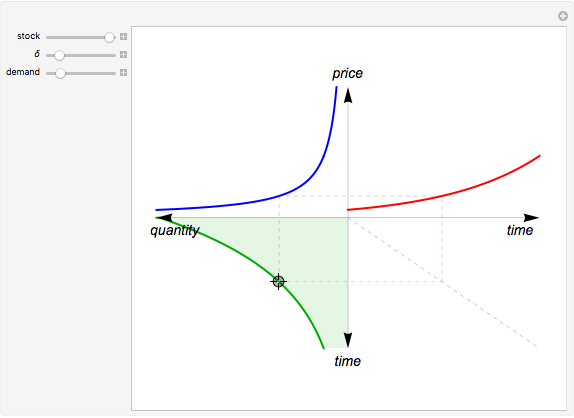
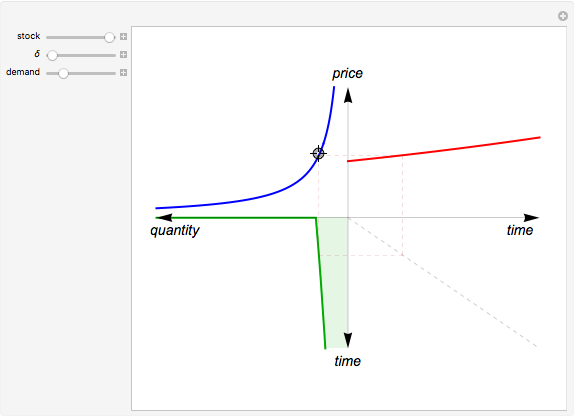
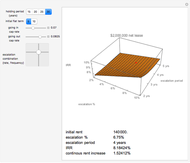
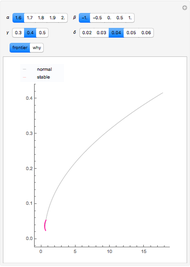
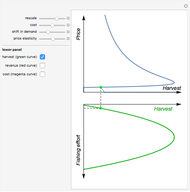
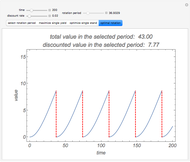
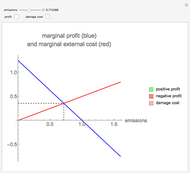
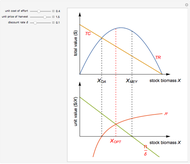
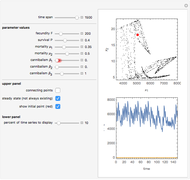
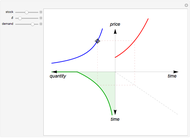
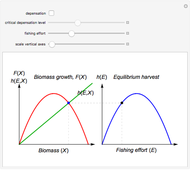
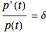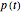The capital-theoretic approach to non-renewable resource economics—as described by Harold Hotelling—is to exhaust the resource over time while maximizing the present value of the resource (Hotelling's rule). This Demonstration illustrates the case of producer market power, indicated by the blue demand curve declining by increasing quantity (note that the quantity axis points to the left).
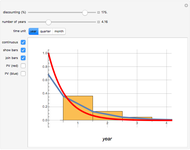
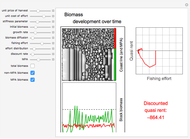
The total resource stock is represented by the shaded area in the lower-left panel enveloped by the green curve, which is the extraction rate. The shadowed area is a finite area, limited by the extraction start (initial extraction value given by the green curve at time zero) and the point of completed stock extraction (the green curve intersects the time axis where the extraction quantity reach zero). Depending on the chosen values, all parts of the finite area defined by the green curve may not be visible within the range of the axes.
The red curve is the optimal price of the resource owner according to the Hotelling’s rule, 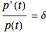 , where
, where 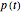 is the unit price of the resource and
is the unit price of the resource and  is the resource owner’s discount rate. In this Demonstration there are no extraction costs.
is the resource owner’s discount rate. In this Demonstration there are no extraction costs.
The shape of the green curve is determined by the stock size and discount rate while the red curve is determined by the discount rate and the demand for the extracted resource. The blue demand curve is in principle given exogenously, influencing the optimal exploitation path of the resource owner.
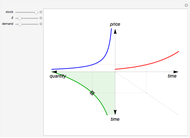
Drag the locator connecting the three curves to study the relation between them. The interconnection between the red, green and blue curves represents a point in time of optimal exploitation according to the given demand, stock size, and discount rate. The shaded area below the dashed line representing the point in time of optimal extraction is the remaining stock size at that very point in time. The capital-theoretic conclusion is that the optimal extraction path is found when the marginal growth in the value of the resource at every point in time equals the discount rate, as stated in the Hotelling's rule.
[less]