Binomial Distributions Are Bernstein Vectors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
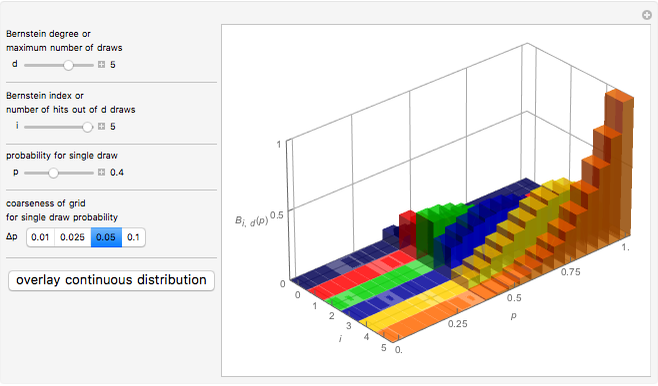
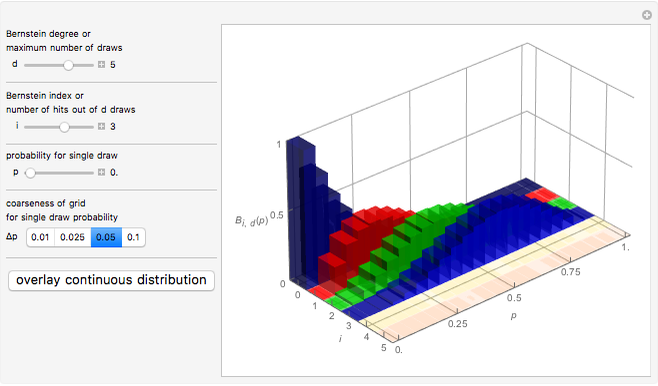
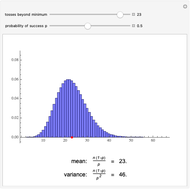
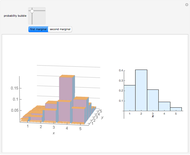
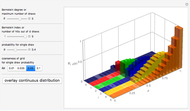
This Demonstration illustrates the intrinsic connection between binomial distributions and Bernstein polynomials. The Bernstein polynomial of degree  and index
and index  ,
, 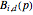 , is equal to the probability of observing
, is equal to the probability of observing 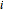 hits in
hits in  identical draws with probability
identical draws with probability 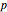 of a hit on each draw.
of a hit on each draw.
Contributed by: Ludwig Weingarten (February 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
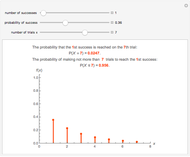
A binomial distribution 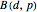 (in Mathematica, the built-in function BinomialDistribution[
(in Mathematica, the built-in function BinomialDistribution[ ,
,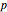 ]), for single-draw probability
]), for single-draw probability 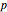 and a maximum number of draws
and a maximum number of draws  , is a vector with
, is a vector with 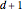 entries (counting from 0 to
entries (counting from 0 to  ).
).
The 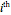 component of this vector gives the probability of having exactly
component of this vector gives the probability of having exactly 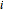 hits in
hits in  draws when a single draw has the probability
draws when a single draw has the probability 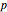 to hit.
This is known to be
to hit.
This is known to be 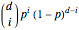 , so the distribution can be seen as a family of vectors indexed by
, so the distribution can be seen as a family of vectors indexed by 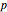 .
For more information, see T. H. Wonnacott and R. J. Wonnacott, Introductory Statistics, 4th ed., New York: Wiley, 1985.
.
For more information, see T. H. Wonnacott and R. J. Wonnacott, Introductory Statistics, 4th ed., New York: Wiley, 1985.
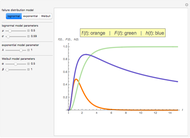
Bernstein polynomials, 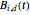 , are weighted multiples of
, are weighted multiples of  and
and  of the form
of the form 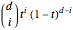 , where
, where  is the degree,
is the degree, 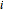 is the index running from 0 to
is the index running from 0 to  , and
, and  . So, for each degree
. So, for each degree  , there are
, there are 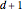 polynomial functions
polynomial functions 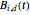 from
from 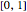 to
to 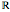 . The only zeros of these functions are 0 and 1; the index
. The only zeros of these functions are 0 and 1; the index 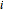 counts the multiplicity of the root at 0 and
counts the multiplicity of the root at 0 and 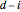 counts the multiplicity of the root at 1. In addition, they are positive in
counts the multiplicity of the root at 1. In addition, they are positive in 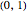 , nonnegative in [0,1] and, for each
, nonnegative in [0,1] and, for each  , they sum to the constant function 1 on
, they sum to the constant function 1 on 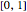 , so they constitute a partition of unity.
, so they constitute a partition of unity.
In Mathematica these polynomials are denoted as BernsteinBasis[d,i,t].
Thinking of the variable  as a probability
as a probability 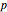 , a Bernstein vector of degree
, a Bernstein vector of degree  and probability
and probability 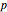 can thus be defined as
can thus be defined as 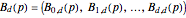 , a vector of functions from
, a vector of functions from 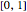 to
to 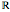 with
with 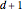 entries.
entries.
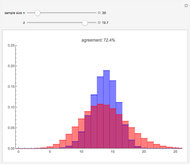
So, for each fixed probability 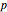 , this
, this 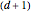 -dimensional Bernstein vector
-dimensional Bernstein vector 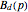 equals the binomial distribution
equals the binomial distribution 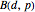 .
.
Permanent Citation