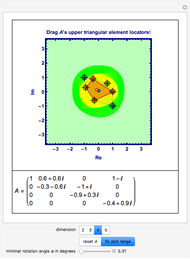
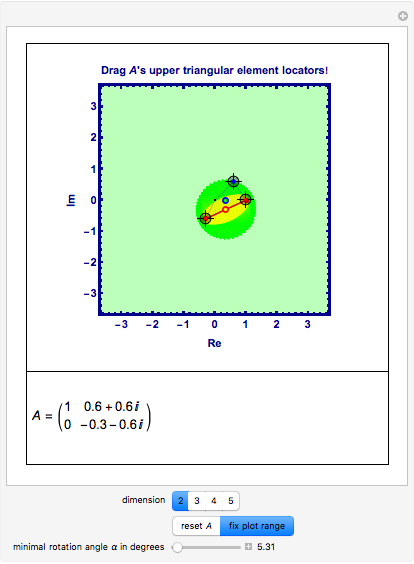
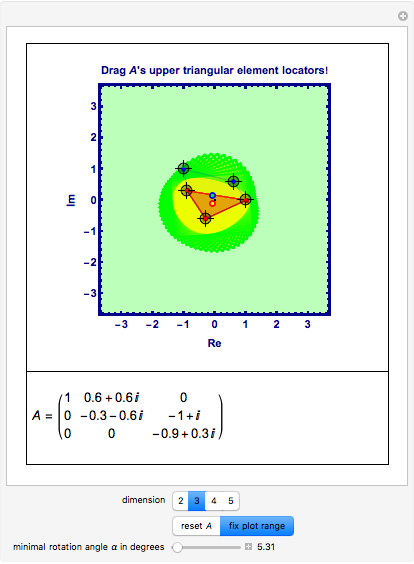
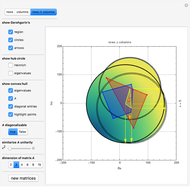
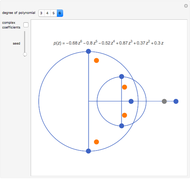
Numerical Range for Some Complex Upper Triangular Matrices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
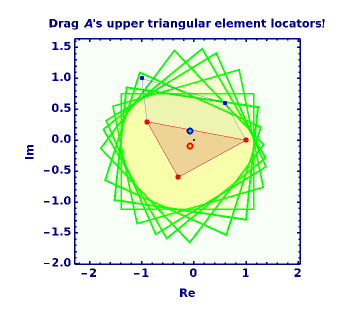
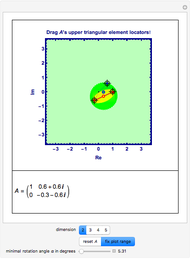
This Demonstration gives a portrait of the neighborhood of the spectrum of a matrix 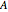 , including an approximation of the numerical range of matrices
, including an approximation of the numerical range of matrices 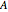 acting in
acting in 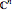 , with low dimension
, with low dimension  .
.
Contributed by: Ludwig Weingarten (December 2010)
Open content licensed under CC BY-NC-SA
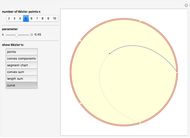
Snapshots
Details
When you try to locate the eigenvalues of complex matrices in the complex plane or to separate characteristic features of nonnormal matrices from normal ones, you inevitably will find terms like field of values, numerical range, Wertebereich, or Rayleigh quotient, and maybe also the important new notion of pseudospectra. These ideas are in part more than a hundred years old, but up to and including Mathematica 7, there are no built-in functions for them. When starting to fill this gap it seems appropriate to give more explanations than usual; more details can be found in any of the books mentioned in the references.
Nonnormal matrices are either deficient, in which case there are not even enough linearly independent eigenvectors to build a basis (never mind an orthonormal basis), or, if they are diagonalizable, lack the property that eigenspaces belonging to different eigenvalues are orthogonal. In the latter case there certainly exists a basis consisting purely of eigenvectors, even normalized ones, but not orthonormal ones. For if they were orthonormalized, some of them would not be eigenvectors anymore, because a linear combination of eigenvectors belonging to different eigenvalues can never be an eigenvector!
Since the Rayleigh quotient is constant on any one-dimensional subspace, it suffices to restrict its domain to the unit ball  , from where it acts as a continuous mapping into the complex numbers.
, from where it acts as a continuous mapping into the complex numbers.
Because the diagonal elements of 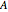 ,
, 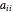 can be found as the Rayleigh quotients of the standard orthonormal basis vectors
can be found as the Rayleigh quotients of the standard orthonormal basis vectors 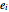 with respect to
with respect to 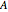 , that is,
, that is, 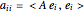 , the whole diagonal of
, the whole diagonal of 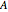 is also part of the field of values, that is,
is also part of the field of values, that is, 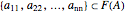 .
.
For a normal matrix 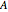 ,
, 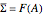 , so that these two sets actually coincide! In this case, the strongest magnification that can occur must take place in the eigenspace belonging to the eigenvalue with the biggest modulus; for all other vectors the magnification will be smaller!
, so that these two sets actually coincide! In this case, the strongest magnification that can occur must take place in the eigenspace belonging to the eigenvalue with the biggest modulus; for all other vectors the magnification will be smaller!
Not so for a nonnormal matrix! In the nonnormal case, the eigenvalue with the biggest modulus must by no means necessarily represent the strongest amplification factor!
Consider, for example, the upper triangular matrix 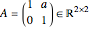 , with
, with  .
. 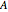 is deficient; it has one two-fold eigenvalue 1, but only one corresponding eigenvector, namely
is deficient; it has one two-fold eigenvalue 1, but only one corresponding eigenvector, namely  , which happens to be just the standard unit vector
, which happens to be just the standard unit vector  . So
. So 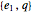 is an orthonormal basis of
is an orthonormal basis of 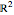 . Let
. Let 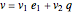 be any vector in
be any vector in 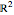 with positive coefficients. Then
with positive coefficients. Then
 .
.
But 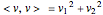 , so
, so  ! And the bigger
! And the bigger  is, the bigger
is, the bigger 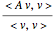 is!
is!
So, for a nonnormal matrix 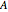 , the knowledge of its spectrum
, the knowledge of its spectrum 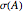 alone might lead to premature conclusions! To be able to understand the action of the underlying mapping, additional information must be taken into account. An important item in that direction will be the determination of the numerical range.
alone might lead to premature conclusions! To be able to understand the action of the underlying mapping, additional information must be taken into account. An important item in that direction will be the determination of the numerical range.
But even for normal matrices 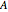 , finding more or less crude supersets of the numerical range is a big gain if one is to enclose the spectrum
, finding more or less crude supersets of the numerical range is a big gain if one is to enclose the spectrum 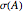 ; see [3], for instance.
; see [3], for instance.
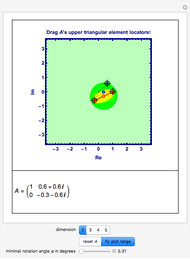
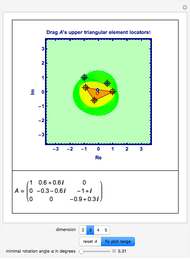
Manipulate Graphic: Get familiar with what is shown! Mouseover the graphics to see explanations, push buttons one after the other; drag any of the locators. After any change, mouseover the graphic again. Almost every item is explained, but some annotations only show up when the respective items are not shadowed by other ones.
References
[1] R. Zurmühl and S. Falk, Matrizen und ihre Anwendungen, Berlin/Heidelberg/New York: Springer–Verlag, 1984.
[2] R. A. Horn and C. R. Johnson, Matrix Analysis, New York: Cambridge University Press, 1985.
[3] R. S. Varga, Gershgorin and His Circles, Berlin/Heidelberg/New York: Springer–Verlag, 2004.
[4] R. A. Horn and C. R. Johnson, Topics in Matrix Analysis, New York: Cambridge University Press, 1991.
[5] L. N. Trefethen and M. Embree, Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators, New Jersey: Princeton University Press, 2005.
Permanent Citation