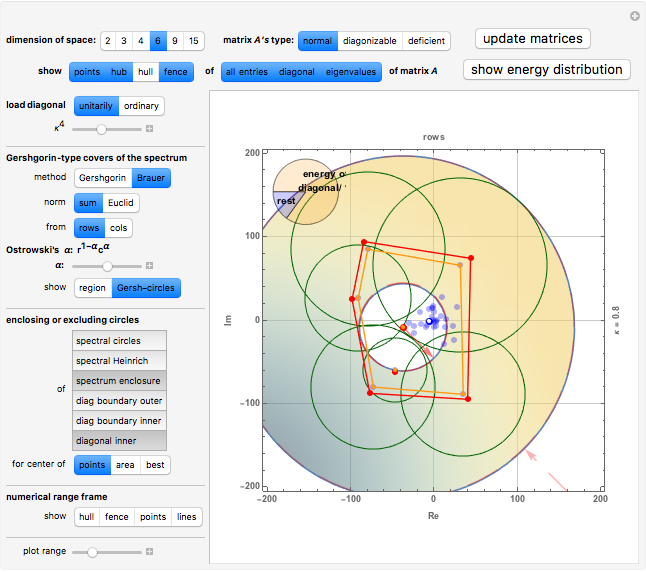
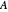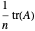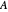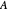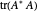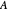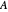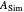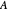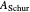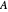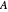Brauer's Cassini Ovals versus Gershgorin Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration gives different views of the neighborhood of the spectrum of a matrix 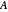 acting in
acting in  , with low dimension
, with low dimension 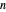 . It continues the ideas presented in the Demonstration "Enclosing the Spectrum by Gershgorin-Type Sets", offering extensions that go by the names of Brauer, Ostrowski, and others.
. It continues the ideas presented in the Demonstration "Enclosing the Spectrum by Gershgorin-Type Sets", offering extensions that go by the names of Brauer, Ostrowski, and others.
Contributed by: Ludwig Weingarten (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration carries on the ideas presented in "Enclosing the Spectrum by Gershgorin-Type Sets", so you are encouraged to read its caption and details.
We want to show as much visual information as possible about the matrix and some easily derivable entities like its hub, its convex hull, the convex hull of its diagonal, its Gershgorin circles, and a lot more, to compare to its spectrum, which is what we are actually looking for, but which is usually a priori not available without huge effort.
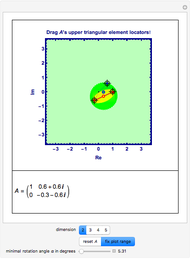
The significance or failure of the concepts for a specific matrix, presented here, should leap to the eyes, especially when using the transition from the matrix  to its Schur similarity
to its Schur similarity 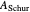 via a unitarized convex combination of its eigenvectors
via a unitarized convex combination of its eigenvectors 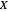 and the identity
and the identity 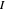 , namely,
, namely, 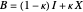 , where the parameter
, where the parameter  varies between 0 and 1;
varies between 0 and 1; 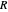 is the orthogonalization of
is the orthogonalization of 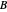 ;
; 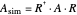 . If the matrix
. If the matrix 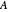 is not normal, this method will not lead to a diagonal similarity, even if the matrix were diagonizable. In this case you can click the "ordinary" button to go over to a version that uses the proper eigensystem to similarize
is not normal, this method will not lead to a diagonal similarity, even if the matrix were diagonizable. In this case you can click the "ordinary" button to go over to a version that uses the proper eigensystem to similarize 
 :
: 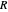 is the normalization of
is the normalization of 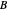 ;
; 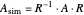 .
In the case of a normal matrix both methods should lead to the same result.
.
In the case of a normal matrix both methods should lead to the same result.
Originally, Gershgorin used a family of disks to cover the spectrum of a matrix
spectrum of a matrix 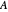 . These disks are derived using seminorms built by the off-diagonal entries of rows or columns.
Brauer refined those ideas to come to what is called "Brauer’s Cassini ovals". These ovals combine two rows or columns at a time to yield a narrower cover than Gershgorin's, at the expense of more labor. Ostrowski showed that combinations of row and column radii could also give closer results.
Using the sum of the squares instead of the absolute values within the seminorms can lead to further refinement, but the covering is not guaranteed to be complete, so it must be taken with care. Most of the ideas presented here are explained in [1], [2], and [3].
. These disks are derived using seminorms built by the off-diagonal entries of rows or columns.
Brauer refined those ideas to come to what is called "Brauer’s Cassini ovals". These ovals combine two rows or columns at a time to yield a narrower cover than Gershgorin's, at the expense of more labor. Ostrowski showed that combinations of row and column radii could also give closer results.
Using the sum of the squares instead of the absolute values within the seminorms can lead to further refinement, but the covering is not guaranteed to be complete, so it must be taken with care. Most of the ideas presented here are explained in [1], [2], and [3].
A single disk, centered at the origin of the complex plane, with a radius called the "spectral radius", will be the most prominent covering of the spectrum of 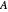 . To show it, you need to know the eigenvalue of
. To show it, you need to know the eigenvalue of 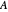 with the biggest modulus. What we show here as "spectral circles" are disks that cover the spectrum of
with the biggest modulus. What we show here as "spectral circles" are disks that cover the spectrum of 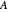 , but whose centers might be taken as the mean of the eigenvalues, that is, the hub, or as the center of area of the convex hull of the eigenvalues, or as the "best" center of the eigenvalues with the smallest radius. Choosing "spectral Heinrich" shows a blue dashed circle centered at the hub of
, but whose centers might be taken as the mean of the eigenvalues, that is, the hub, or as the center of area of the convex hull of the eigenvalues, or as the "best" center of the eigenvalues with the smallest radius. Choosing "spectral Heinrich" shows a blue dashed circle centered at the hub of  . Its diameter is derived from the Frobenius norm of
. Its diameter is derived from the Frobenius norm of 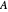 , which overestimates the spectral norm of
, which overestimates the spectral norm of 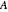 but can be calculated simply from the entries of
but can be calculated simply from the entries of  directly (see [1], p. 237, where it is attributed to Heinrich). It serves as an a priori estimate of the spectral circle.
directly (see [1], p. 237, where it is attributed to Heinrich). It serves as an a priori estimate of the spectral circle.
The next circles are all based on the location of the diagonal entries of 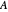 :
• The button "spectrum enclosure" shows a single disk enclosing the spectrum that is based on the Gershgorin circles that are actually chosen.
• The button "diag boundary outer" shows the circle that encloses the whole diagonal of
:
• The button "spectrum enclosure" shows a single disk enclosing the spectrum that is based on the Gershgorin circles that are actually chosen.
• The button "diag boundary outer" shows the circle that encloses the whole diagonal of  .
• The button "diag boundary inner" shows the circle that excludes those diagonal entries of
.
• The button "diag boundary inner" shows the circle that excludes those diagonal entries of 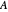 that are on the boundary of the convex hull of the diagonal.
• The button "diagonal inner" shows the circle that excludes the whole diagonal of
that are on the boundary of the convex hull of the diagonal.
• The button "diagonal inner" shows the circle that excludes the whole diagonal of 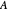 .
.
These four circles can all be determined for different centers. You may show them for the mean of the diagonal entries (the hub), the center of area of the convex hull of the diagonal entries, or the "best" center of the diagonal entries with the smallest radius. When changing from the matrix 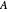 to its Schur similarity
to its Schur similarity 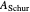 these four circles build a sandwich of circular rings that squeeze the spectrum.
these four circles build a sandwich of circular rings that squeeze the spectrum.
The "numerical range frame" shows a simple framed rectangle that covers the spectrum. To determine it you have to calculate at least four eigenvalues, the minimum and maximum of the Hermitian part of 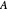 and the minimum and maximum of the skew-Hermitian part of
and the minimum and maximum of the skew-Hermitian part of 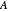 . This is possible, since each of these two parts is Hermitian, and so has only real eigenvalues. Clicking "points" positions all the eigenvalues of these two parts at appropriate locations on the frame,
whereas "lines" gives a grid whose crossings are built from all possible pairs of eigenvalues of these two parts.
. This is possible, since each of these two parts is Hermitian, and so has only real eigenvalues. Clicking "points" positions all the eigenvalues of these two parts at appropriate locations on the frame,
whereas "lines" gives a grid whose crossings are built from all possible pairs of eigenvalues of these two parts.
Note: A matrix 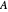 is normal exactly when its Hermitian part and its skew-Hermitian part commute. In that case, the real part of its spectrum coincides with the spectrum of its Hermitian part and the imaginary part of its spectrum coincides with the spectrum of its skew-Hermitian part; so these two real spectra are just the projections of the spectrum of
is normal exactly when its Hermitian part and its skew-Hermitian part commute. In that case, the real part of its spectrum coincides with the spectrum of its Hermitian part and the imaginary part of its spectrum coincides with the spectrum of its skew-Hermitian part; so these two real spectra are just the projections of the spectrum of 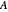 onto the real and imaginary axes. Or, conversely, the eigenvalues of
onto the real and imaginary axes. Or, conversely, the eigenvalues of 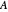 can all be found under the crossings of the lines. If
can all be found under the crossings of the lines. If 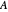 is not normal, you can only claim that the respective two real numerical ranges are just the projections of the numerical range of
is not normal, you can only claim that the respective two real numerical ranges are just the projections of the numerical range of  onto the real and imaginary axes; the eigenvalues of
onto the real and imaginary axes; the eigenvalues of 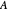 cannot, in general, be found within those crossings.
cannot, in general, be found within those crossings.
To learn more about the concept of the numerical range, see the Demonstration "Numerical Range for Some Complex Upper Triangular Matrices"and consult [4] or [5].
All matrices in the snapshots are normal.
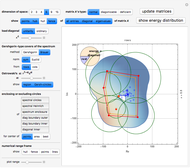
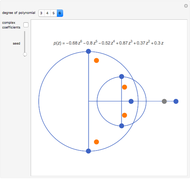
Brauer's covering and Gershgorin's circles
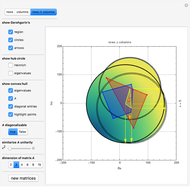
Snapshot 1: all entries, diagonal entries plus eigenvalues of the original matrix 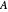 , their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, Brauer's covering
, their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, Brauer's covering
Snapshot 2: all entries, diagonal entries plus eigenvalues of the similarity 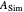 of
of  , for
, for 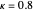 , their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, Brauer's covering
, their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, Brauer's covering
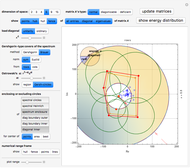
Spectrum squeezing circles, centered at the hub
Snapshot 3: all entries, diagonal entries plus eigenvalues of the similarity 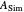 of
of 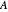 , for
, for 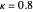 , their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, spectrum squeezing circles, centered at the hub
, their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, spectrum squeezing circles, centered at the hub
Numerical range frame
Snapshot 4: all entries, diagonal entries plus eigenvalues of the original matrix 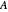 , their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, numerical range frame, plus eigenvalues of Hermitian and skew-Hermitian parts, plus their intersecting lines
, their means and their convex hull fences, the energy distribution between the diagonal and the rest, Gershgorin's circles, numerical range frame, plus eigenvalues of Hermitian and skew-Hermitian parts, plus their intersecting lines
References
[1] R. Zurmühl and S. Falk, Matrizen und ihre Anwendungen, Berlin/Heidelberg/New York: Springer–Verlag, 1984.
[2] R. A. Horn and C. R. Johnson, Matrix Analysis, New York: Cambridge University Press, 1985.
[3] R. S. Varga, Gershgorin and His Circles, Berlin/Heidelberg/New York: Springer–Verlag, 2004.
[4] R. A. Horn and C. R. Johnson, Topics in Matrix Analysis, New York: Cambridge University Press, 1991.
[5] L. N. Trefethen and M. Embree, Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators, Princeton, NJ: Princeton University Press, 2005.
Permanent Citation