Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Biregular Star Graphs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

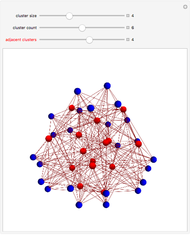
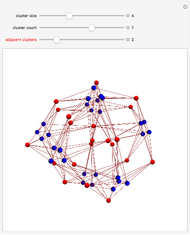
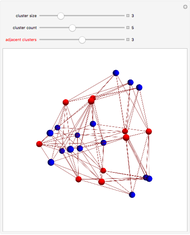
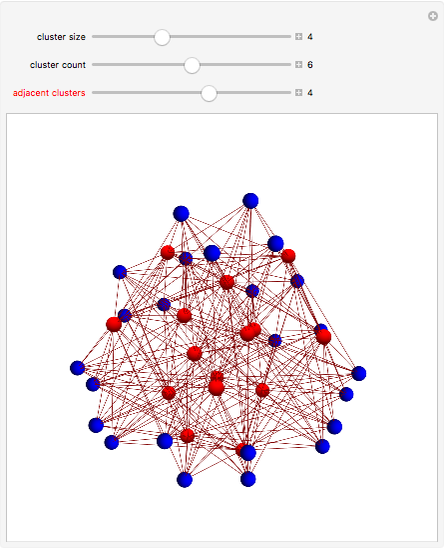
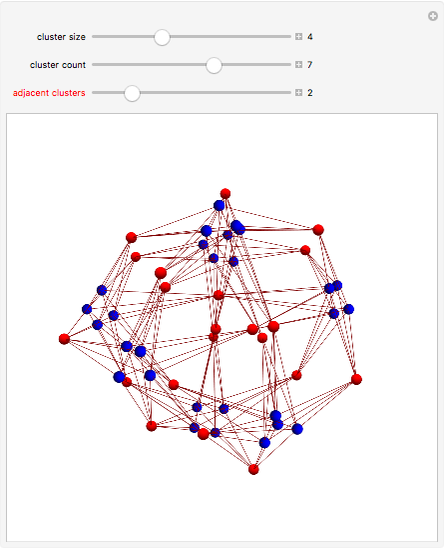
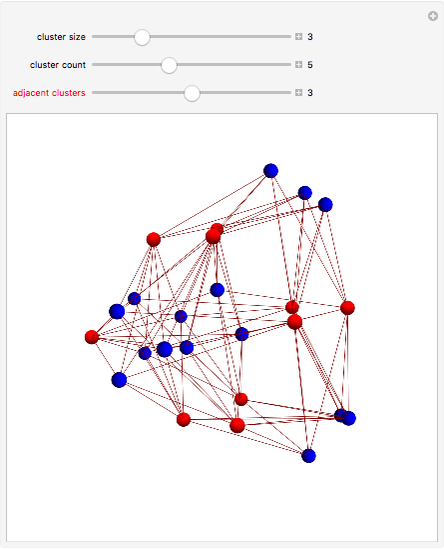
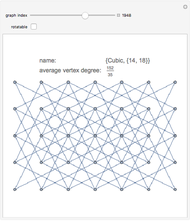
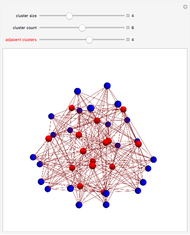
This Demonstration shows a family of biregular graphs that arise in the study of inverse problems on electrical networks. The blue nodes are boundaries and the red nodes are interiors. The sliders control the size of the blue clusters, the total number of blue clusters, and the number of clusters incident to any red node.

[more]

Each of these graphs is called a "star". There is a transformation that yields an electrically equivalent "K" network. Studying the "K" network allows one to determine recoverability properties of the inverse problem. For more information, see [1] in the Details section.

Biregular graphs such as these arise in projective geometry due to the Levi graph construction.

[less]

Contributed by: Avi Levy (August 2014)
With additional contributions by: Jim Morrow, Katherine Lacy, and Molly Baird
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] A. Levy. "Biregular Networks." (Jul 20, 2014) www.math.washington.edu/~avius/biregular.pdf.

[2] University of Washington. "REU Summer 2014 Inverse Problems." (2014) www.math.washington.edu/~reu.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send