Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

3D Unit-Distance Graphs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

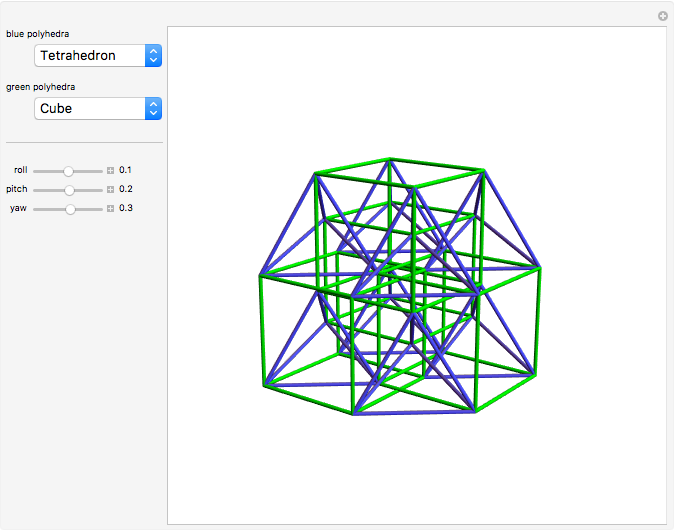
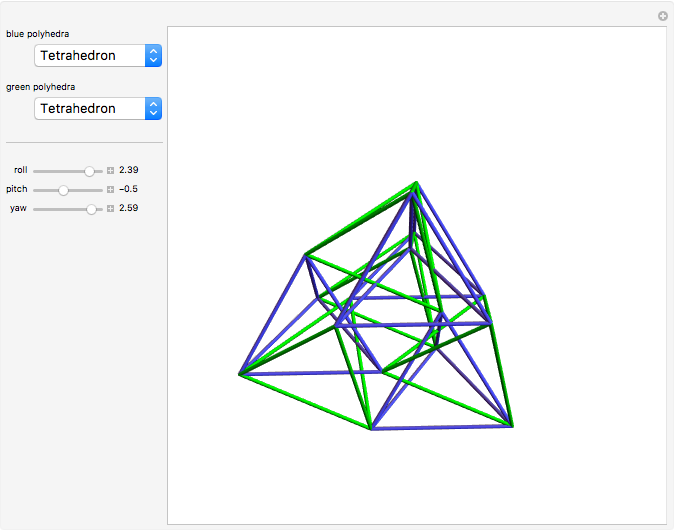
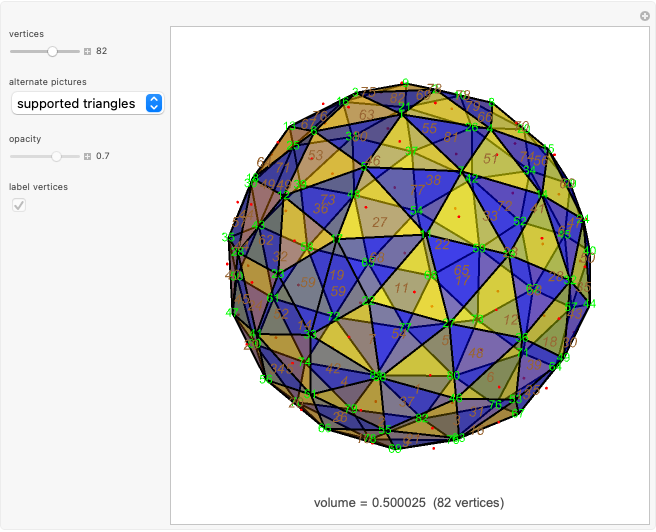
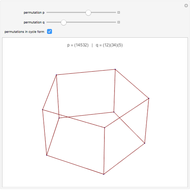
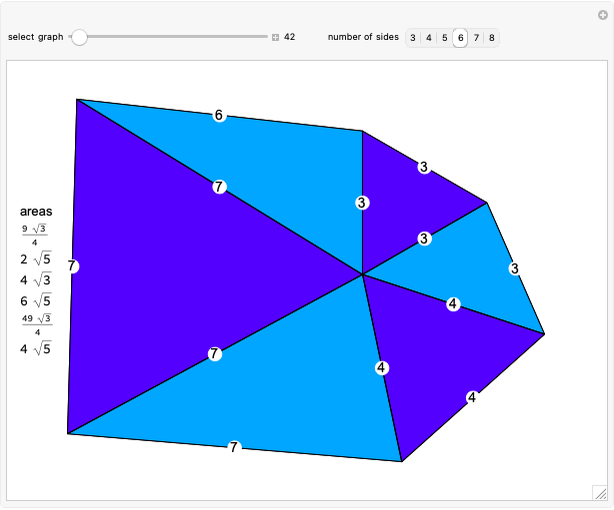
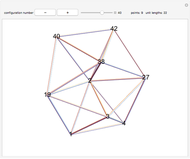
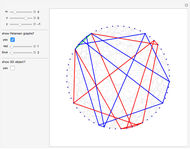
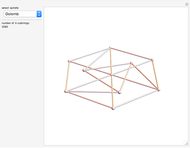
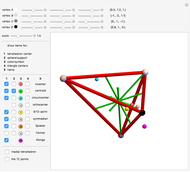
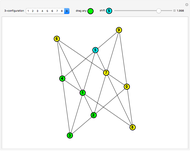
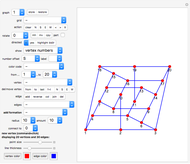
In two dimensions, the Harborth graph has four unit-length edges meeting at each vertex. In other words, it has valency four. In three dimensions, the octahedron has valency four. The icosahedron has valency five. What about valency six?

[more]

This Demonstration combines smaller polyhedral graphs to obtain larger unit distance with high valency. This combination method is sometimes called the graph product.

You can vary the roll, pitch, and yaw (in radians) on the graphic.

[less]

Contributed by: Ed Pegg Jr (October 2015)
Open content licensed under CC BY-NC-SA

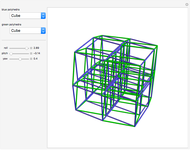
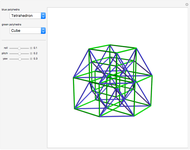
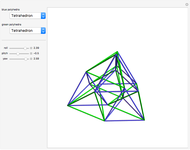
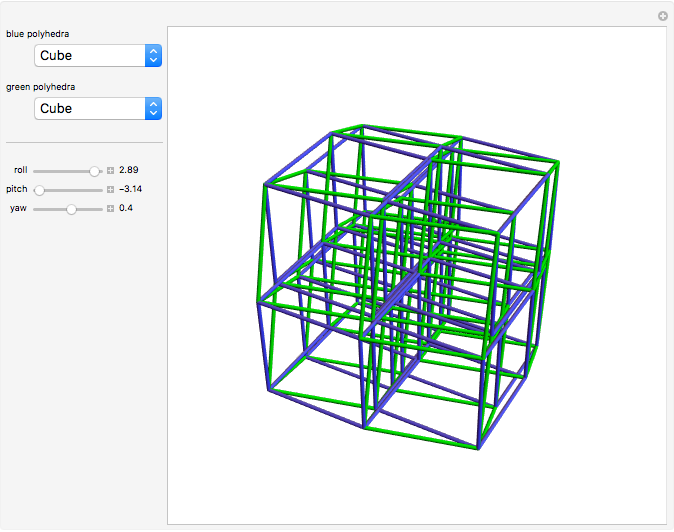
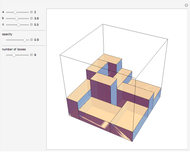
Snapshots

Details

In 2D, whether the Harborth graph is the smallest graph with valency four is an unsolved question. In 3D, for valency 6–10, the methods in this Demonstration can generate unit-distance graphs with 16, 24, 36, 64, and 96 vertices, but there are likely smaller such graphs. For valency 10, use tetrahedron × tetrahedron × octahedron.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send