Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bound-State Spectra for Two Delta Function Potentials

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

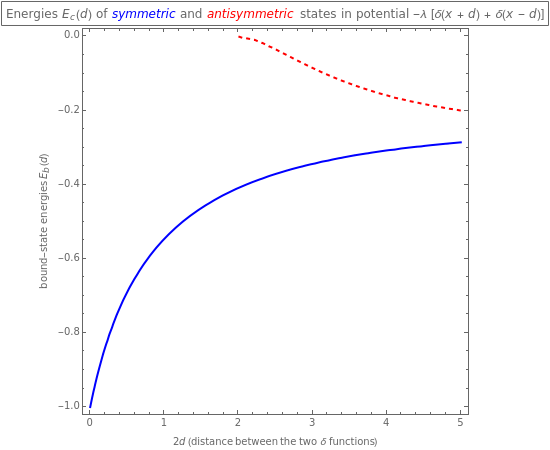
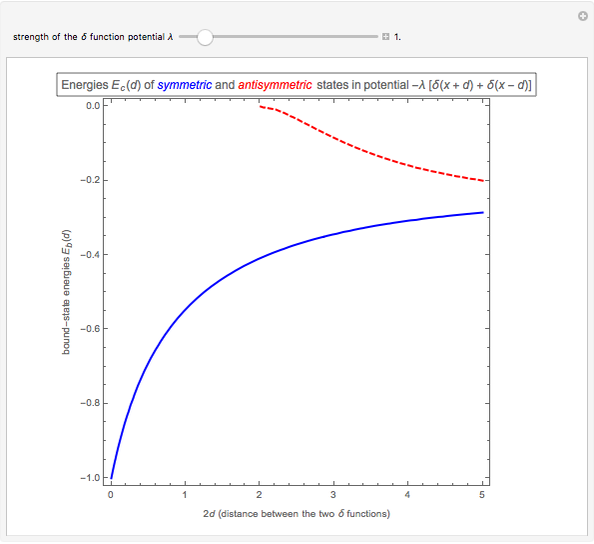
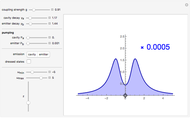
This Demonstration shows the bound-state spectra 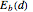of a particle of mass 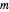in the presence of two attractive potentials separated by a distance 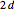, 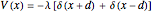. Since the Fourier transform of this potential is factorizable, 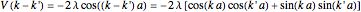, the bound-state spectra are easily obtained using the momentum-space Schrödinger equation. The energies are normalized to the magnitude of the symmetric-state energy at . Note that the second (antisymmetric) bound state appears only when the distance between the functions exceeds the critical value .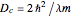

Contributed by: Christopher R. Jamell and Yogesh N. Joglekar (IUPUI) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

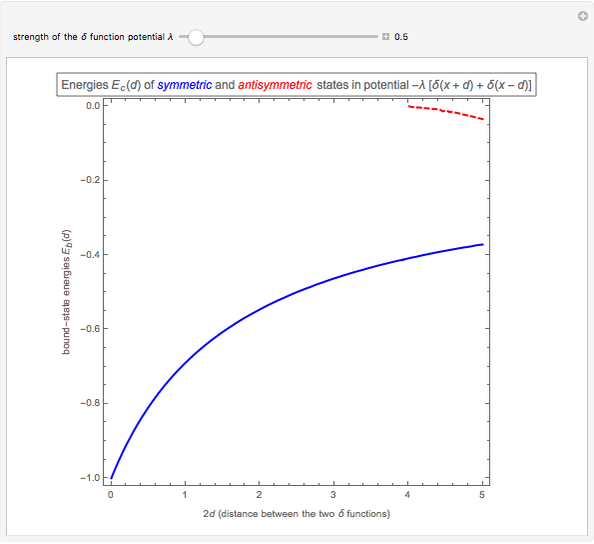
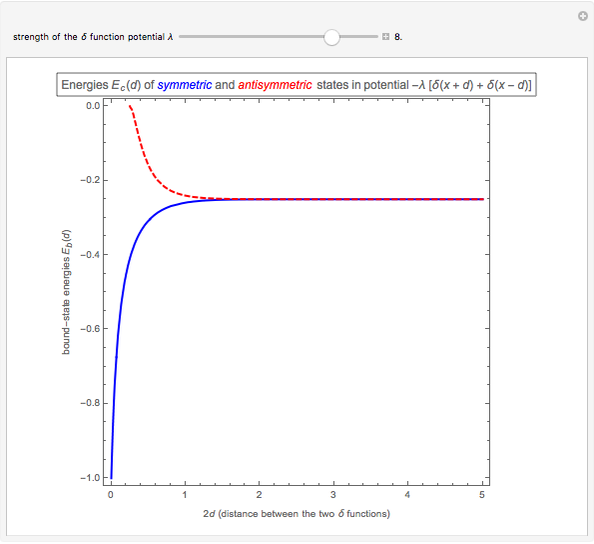
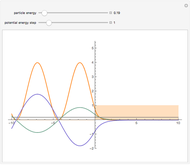
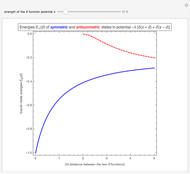
Snapshot 1: typical symmetric and antisymmetric bound-state energies as a function of distance 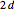between the two attractive functions

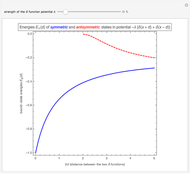
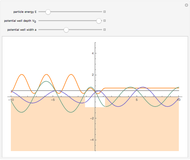
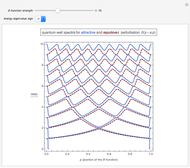
Snapshot 2: for a weak potential strength 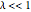, a second bound-state, the antisymmetric state, appears only when the distance between the two functions is large,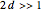

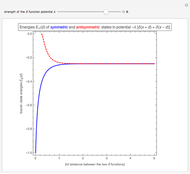
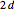Snapshot 3: for a strong potential , the symmetric and antisymmetric states become degenerate when the distance between the two functions is increased

Analytical and numerical treatment of the Schrodinger equation in momentum space can be found in W. A. Karr, C. R. Jamell, and Y. N. Joglekar, "Numerical Approach to Schrodinger Equation in Momentum Space," arXiv, 2009.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send