Entanglement between a Two-Level System and a Quantum Harmonic Oscillator

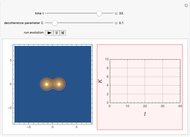
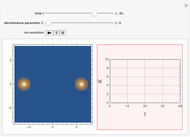
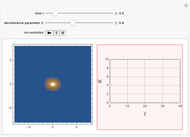
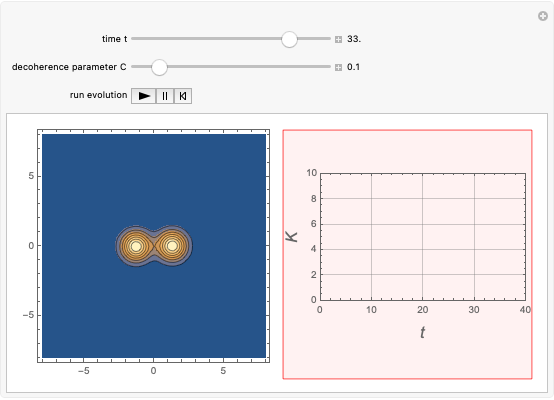
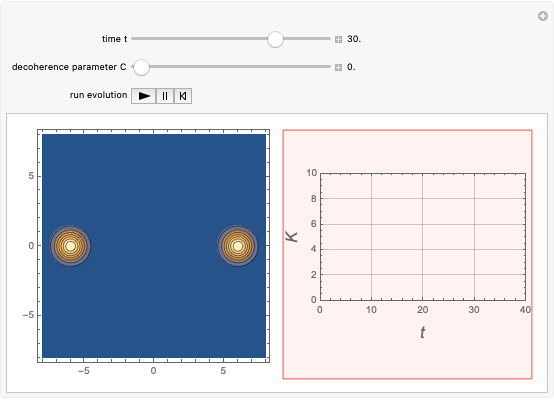
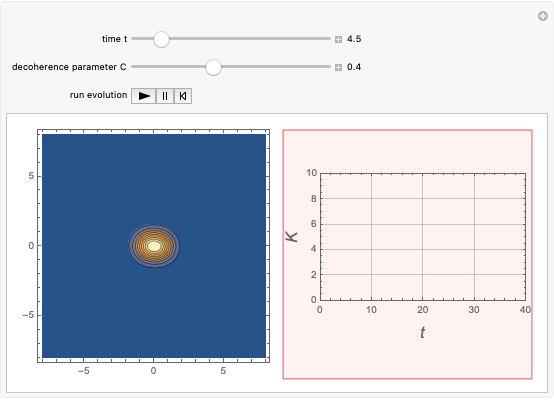
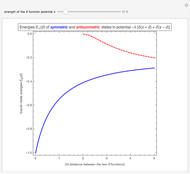
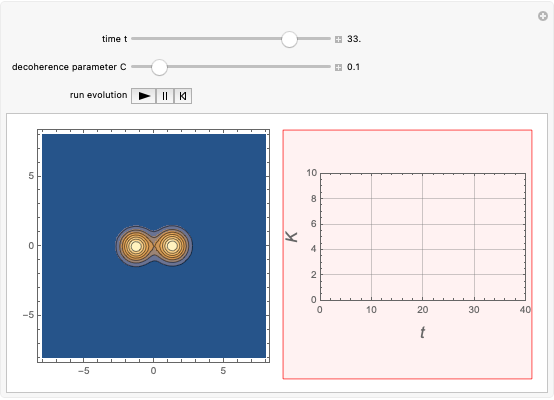
This Demonstration shows the time-evolution (the Glauber-Sudarshan representation of the oscillator over time) and the participation ratio (a measure of the entanglement) of a system that consists of a quantum harmonic oscillator coupled with a delta pulse applied to a two-level system. The system is originally unentangled and in thermal equilibrium with the environment. The parameter 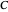, the decoherence parameter, depends on the strength of the coupling of the system with a Markovian bath.

The entanglement of a system is the quantum correlation between the two subsystems, which is measured by various quantities such as von Neumann entropy, participation ratio, negativity, etc. The entanglement is stronger when the two Gaussian peaks are further apart and have fewer mixed parts. The Demonstration shows that the decoherence would eventually dissipate the entanglement.