Soliton Trajectories of the Modified Korteweg-de Vries Equation (mKdV)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
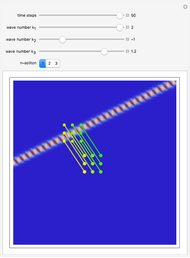
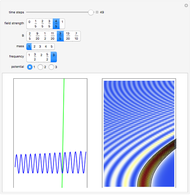
According to the Bohmian interpretation of quantum theory, often called today "causal de Broglie-Bohm theory", it is possible to allocate trajectories of idealized particles to waves. In this Demonstration the mKdV equation is studied to show how the velocity field guides the particles inside a two-soliton. From the mKdV, 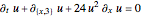 , the continuity equation
, the continuity equation  is derived via
is derived via  , where
, where  is the velocity field and
is the velocity field and  is the wave amplitude. As the value of the velocity is known at each time, the evolution of Bohmian trajectories is obtained by numerical integration for different initial positions. The two-soliton implies that the higher amplitude wave is narrower and faster than the wave with the minor amplitude. The trajectories of the individual solitons show that in the two-soliton collision the amplitude and the velocity are exchanged, rather than passing through one another. The system is time reversible:
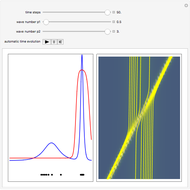
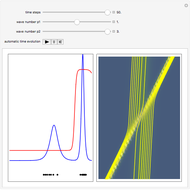
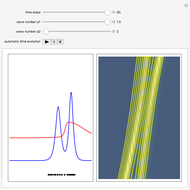
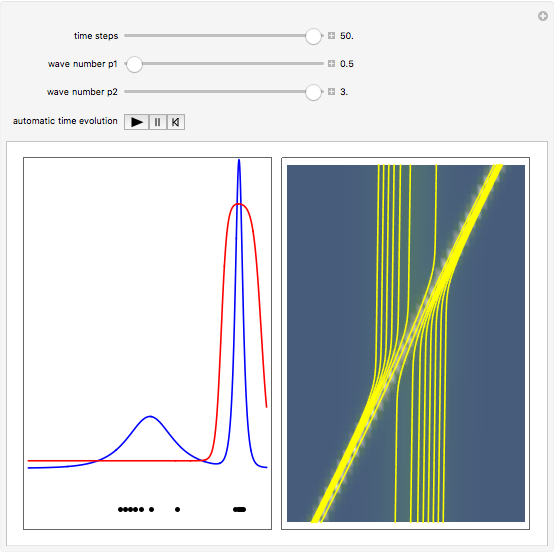
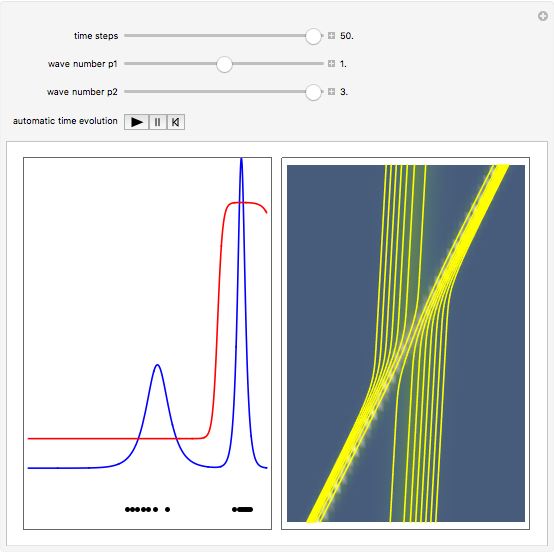
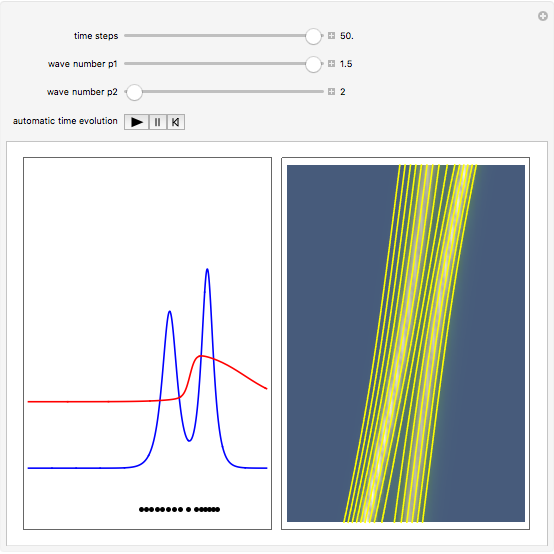
is the wave amplitude. As the value of the velocity is known at each time, the evolution of Bohmian trajectories is obtained by numerical integration for different initial positions. The two-soliton implies that the higher amplitude wave is narrower and faster than the wave with the minor amplitude. The trajectories of the individual solitons show that in the two-soliton collision the amplitude and the velocity are exchanged, rather than passing through one another. The system is time reversible:  . On the left you can see the position of the particles, the wave amplitude (blue), and the velocity (red). On the right the graphic shows the wave amplitude and the complete trajectories in
. On the left you can see the position of the particles, the wave amplitude (blue), and the velocity (red). On the right the graphic shows the wave amplitude and the complete trajectories in 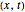 space. The velocity is scaled to fit.
space. The velocity is scaled to fit.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
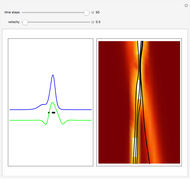
Snapshots
Details
The wave amplitude 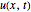 is taken from: A. Pekcan, "The Hirota Direct Method," master's thesis, Bilkent University, Turkey, 2005.
is taken from: A. Pekcan, "The Hirota Direct Method," master's thesis, Bilkent University, Turkey, 2005.
Permanent Citation