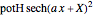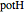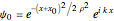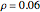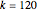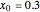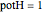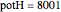Radioactive Decay in the Causal Interpretation of Quantum Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
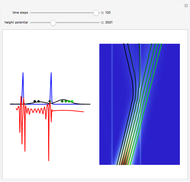
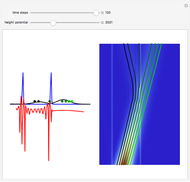
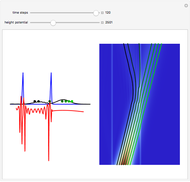
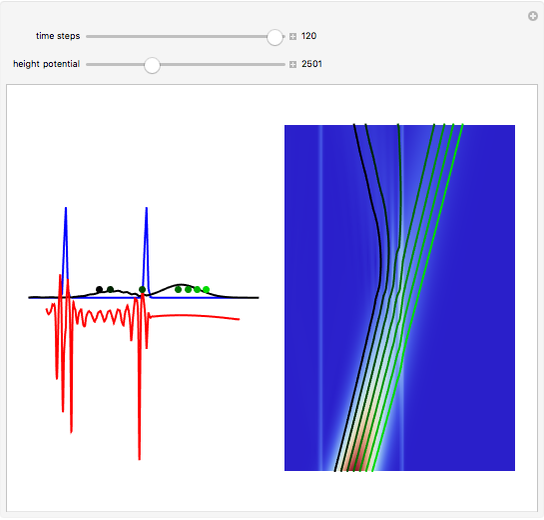
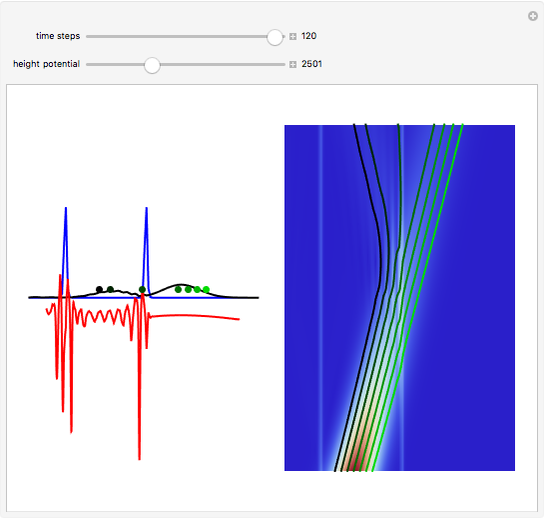
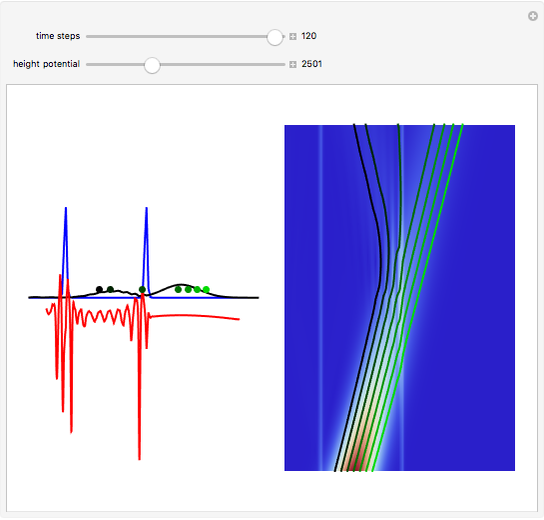
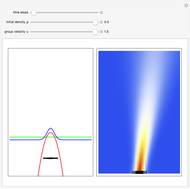
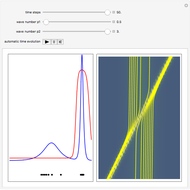
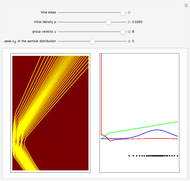
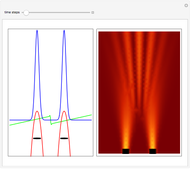
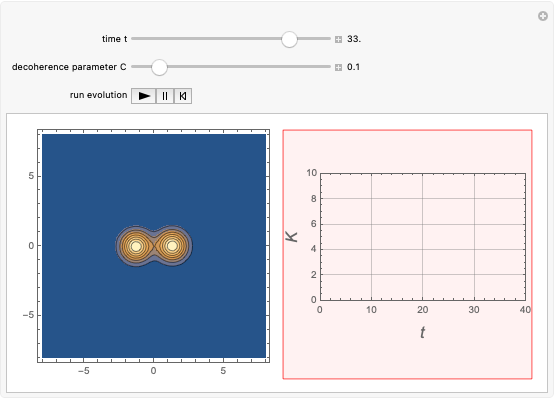
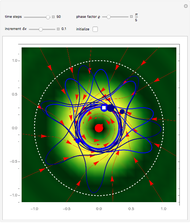
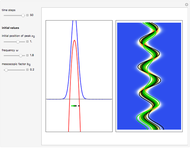
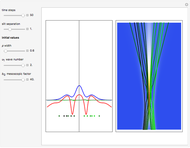
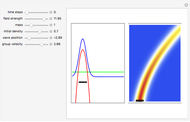
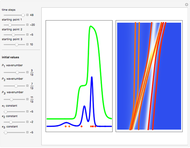
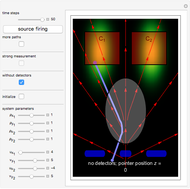
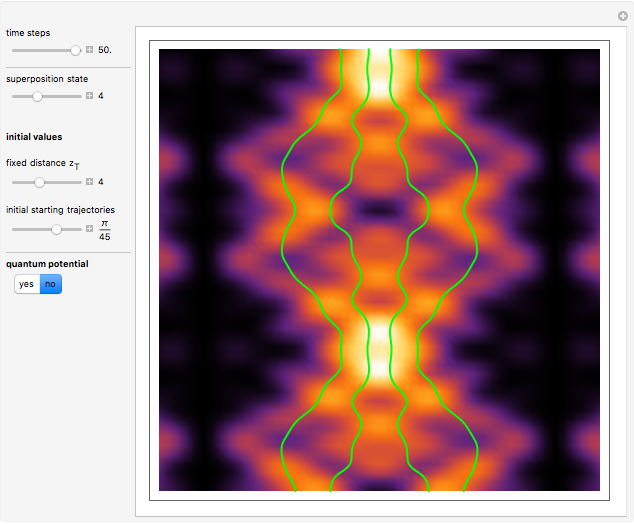
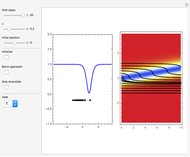
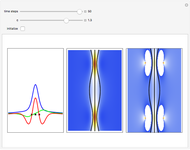
According to classical physics, a particle can never overcome a potential greater than its kinetic energy; this is not the case in quantum theory. For unstable isotopes there is a finite probability for a quantum particle (an  particle) to tunnel through the potential barrier in a nucleus. Such isotopes are called radioactive isotopes. The behavior of such isotopes can be described by a square wave packet that is a solution of the Schrödinger equation with the potential term
particle) to tunnel through the potential barrier in a nucleus. Such isotopes are called radioactive isotopes. The behavior of such isotopes can be described by a square wave packet that is a solution of the Schrödinger equation with the potential term 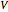 . The time evolution leads to a wave packet that bounces back and forth. Each time it strikes the potential barrier a part of the packet tunnels through and there is a chance for some transmission. In orthodox quantum theory it is impossible to predict the decay of a single isotope. A statistical conclusion can be made only for an ensemble of isotopes (e.g., half-life period).
. The time evolution leads to a wave packet that bounces back and forth. Each time it strikes the potential barrier a part of the packet tunnels through and there is a chance for some transmission. In orthodox quantum theory it is impossible to predict the decay of a single isotope. A statistical conclusion can be made only for an ensemble of isotopes (e.g., half-life period).
Contributed by: Klaus von Bloh (December 2008)
Based on a program by: Enrique Zeleny and Paul Nylander
Open content licensed under CC BY-NC-SA
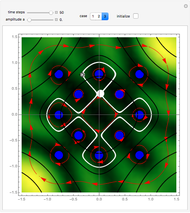
Snapshots
Details
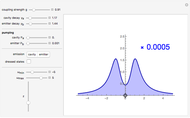
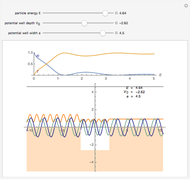
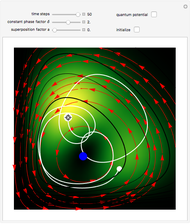
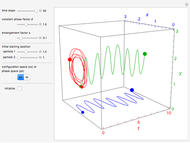
The guidance equation for the particle velocity is 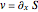 , which is calculated from the gradient of the phase from the total wavefunction in the eikonal form
, which is calculated from the gradient of the phase from the total wavefunction in the eikonal form 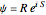 . The quantum potential
. The quantum potential 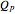 is given by
is given by 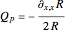 . The effective potential is the sum of quantum potential and nuclear potential that leads to the time-dependent quantum force:
. The effective potential is the sum of quantum potential and nuclear potential that leads to the time-dependent quantum force: 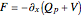 . The numerical methods to calculate the velocity and the quantum potential from a discrete function are, in general, not very stable, but the applied interpolation functions lead to an accurate approximation of the physical event; due to the numerical errors produced by the limited mesh of 120 mesh points, the velocity term must be adjusted (here using 41/100 instead of 0.5).
. The numerical methods to calculate the velocity and the quantum potential from a discrete function are, in general, not very stable, but the applied interpolation functions lead to an accurate approximation of the physical event; due to the numerical errors produced by the limited mesh of 120 mesh points, the velocity term must be adjusted (here using 41/100 instead of 0.5).
References
C. Dewdney and B. J. Hiley, "A Quantum Potential Description of One-Dimensional Time-Dependent Scattering from Square Barriers and Square Wells," Found. Phys. 12(1), 1982 pp. 27–48.
J. Caulfield, "What Determines Alpha Decay?," Portsmouth Polytechnic (England), student research project, unpublished, 1991.
A. Goldberg, H. Schey, and J. L. Schwartz, "Computer-Generated Motion Pictures of One-Dimensional Quantum Mechanical Transmission and Reflection Phenomena," Am. J. Phys., 35(3), 1967 pp. 177–186.
Permanent Citation