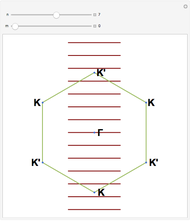
Brillouin Zone Sampling of a Periodic Chain with N Sites

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
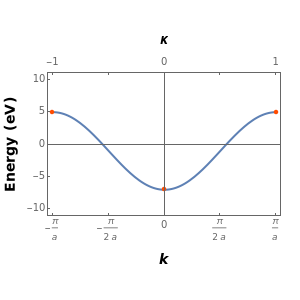
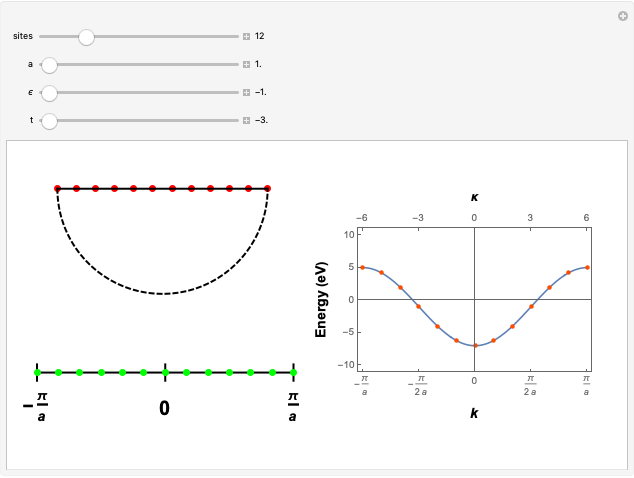
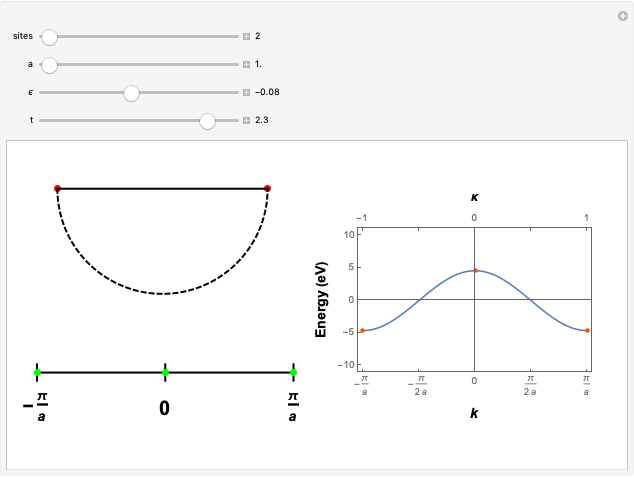
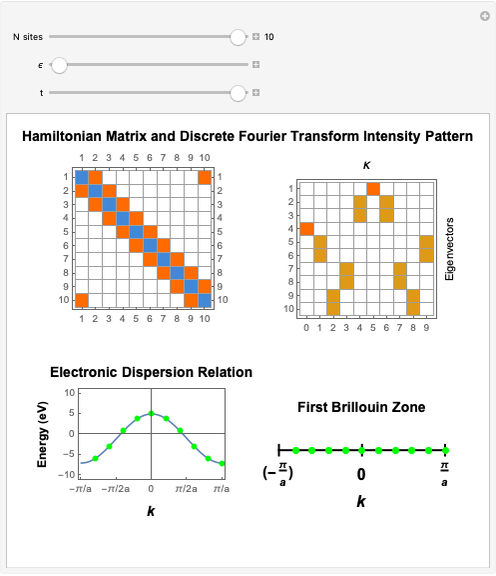
This Demonstration shows the sampling of the  -points in the first Brillouin zone (BZ) of a virtually infinite linear crystal as a function of the number of sites in the unit cell. By choosing a periodic chain with
-points in the first Brillouin zone (BZ) of a virtually infinite linear crystal as a function of the number of sites in the unit cell. By choosing a periodic chain with 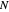 sites one can sample
sites one can sample 
 -points in the reciprocal space of the first BZ, whose spacing is inversely proportional to
-points in the reciprocal space of the first BZ, whose spacing is inversely proportional to 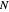 and the lattice parameter
and the lattice parameter 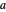 . Then
. Then 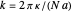
 , where
, where  is the allowed quantum number for the chain (
is the allowed quantum number for the chain (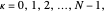 or equivalently,
or equivalently, 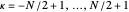 ). There is also cyclic periodicity in
). There is also cyclic periodicity in 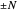 . The
. The  -points thus obtained are mapped onto the analytical form of the tight-binding electronic dispersion relation
-points thus obtained are mapped onto the analytical form of the tight-binding electronic dispersion relation 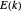 for the chain. Diagonalizing the associated Bloch Hamiltonian gives the electronic energy eigenvalues
for the chain. Diagonalizing the associated Bloch Hamiltonian gives the electronic energy eigenvalues 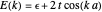 . These are calculated and plotted as a function of the tight-binding hopping parameter
. These are calculated and plotted as a function of the tight-binding hopping parameter  and the on-site energy parameter
and the on-site energy parameter  expressed in electron volts.
expressed in electron volts.
Contributed by: Jessica Alfonsi (University of Padova, Italy) (March 2011)
Open content licensed under CC BY-NC-SA
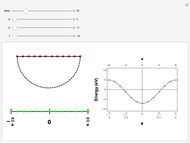
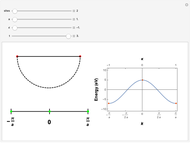
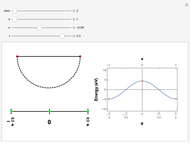
Snapshots
Details
C. Kittel, Introduction to Solid State Physics, 7th ed., Hoboken, New Jersey: J. Wiley and Sons, 1996.
S. L. Altmann, Band Theory of Solids: An Introduction from the Point of View of Symmetry, Oxford: Clarendon Press, 1991.
J. Alfonsi, Small Crystal Models for the Electronic Properties of Carbon Nanotubes, PhD thesis, University of Padova, 2009, Chap. 4 and references therein.
Permanent Citation