Brillouin Zone Sampling of Chain with N Sites and Modified Periodic Boundary Conditions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
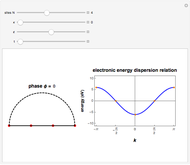
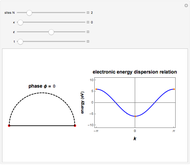
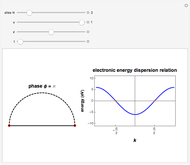
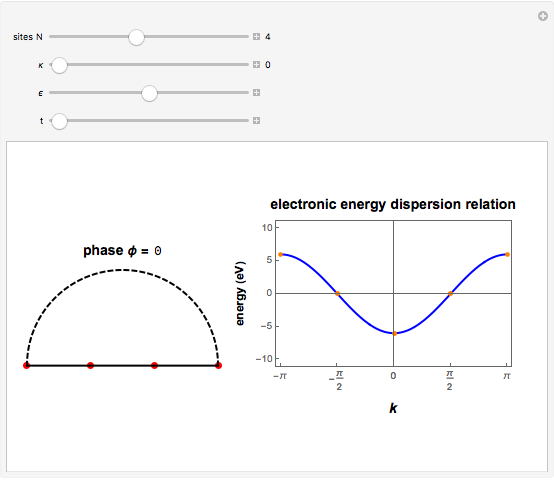
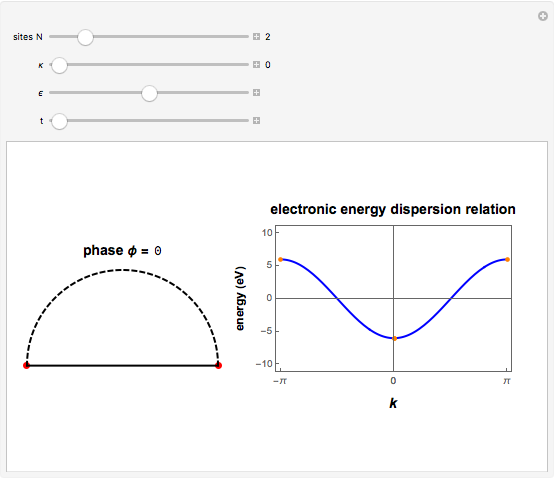
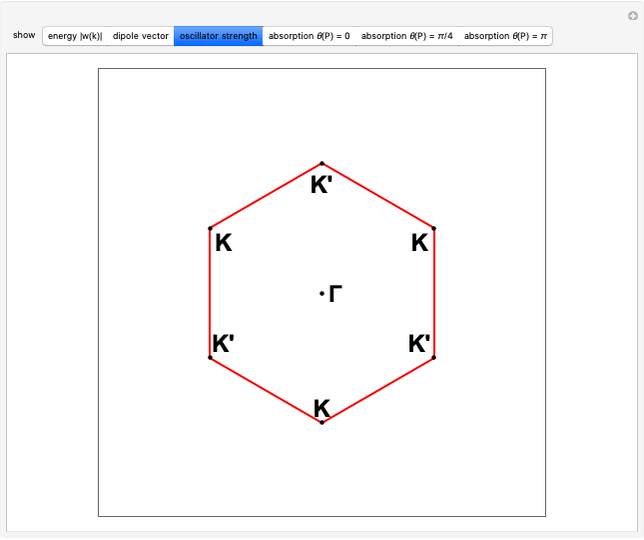
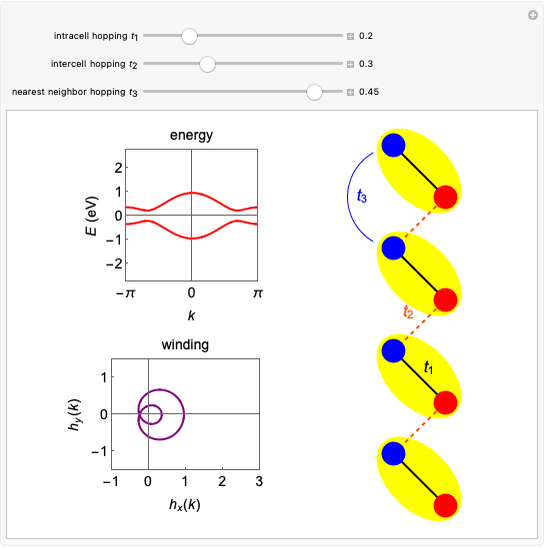
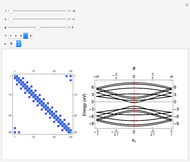
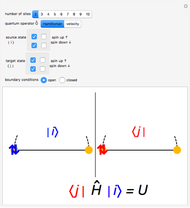
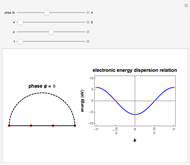
This Demonstration shows the use of a complex exponential phase factor in the periodic boundary conditions of the Wannier tight-binding (TB) Hamiltonian of a chain with 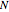 sites, TB hopping parameter
sites, TB hopping parameter  , and on-site energy parameter
, and on-site energy parameter  . This requires modified periodic boundary conditions (MPBCs). The phase is given by
. This requires modified periodic boundary conditions (MPBCs). The phase is given by 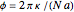 , where
, where 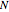 is the number of sites,
is the number of sites, 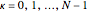 , and
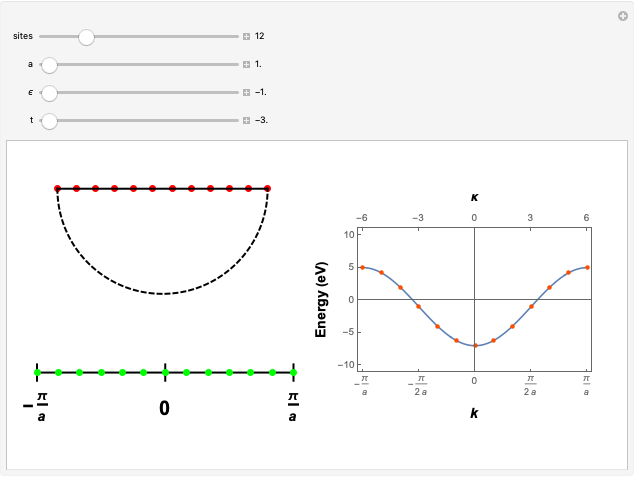
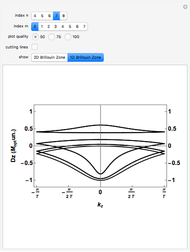
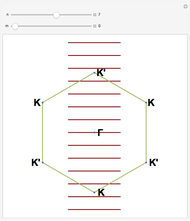
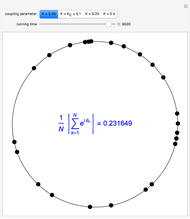
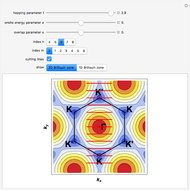
, and  is the lattice parameter of the chain. The use of MPBCs allows sampling other points inside the first Brillouin zone (BZ) with a small number of sites, which otherwise could only be reached by choosing a system with a higher number of sites. For instance, the points sampled with four sites can also be obtained with a two-site chain and switching the phase
is the lattice parameter of the chain. The use of MPBCs allows sampling other points inside the first Brillouin zone (BZ) with a small number of sites, which otherwise could only be reached by choosing a system with a higher number of sites. For instance, the points sampled with four sites can also be obtained with a two-site chain and switching the phase  between the allowed values
between the allowed values  and
and  . When
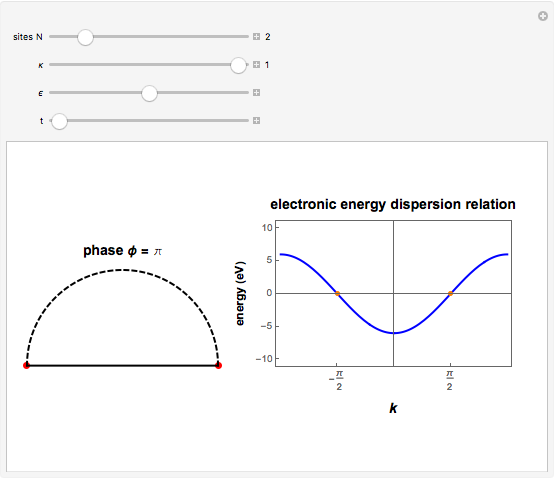
. When  , the MPBCs are simply periodic boundary conditions, while for
, the MPBCs are simply periodic boundary conditions, while for  the MPBCs are anti-periodic boundary conditions (APBCs). This trick of sweeping
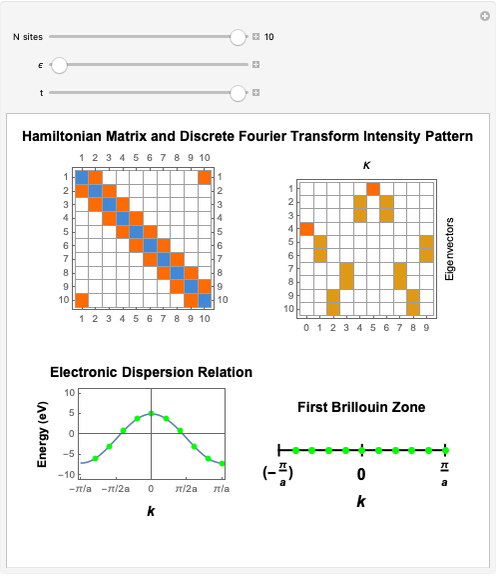
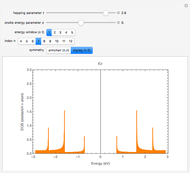
the MPBCs are anti-periodic boundary conditions (APBCs). This trick of sweeping  is particularly important and useful in the field of strongly correlated electron systems, where one has to perform exact diagonalizations of huge matrices (e.g., Hubbard-like matrices) for investigating the BZ with the aid of finite-sized systems having a very small number of sites.
is particularly important and useful in the field of strongly correlated electron systems, where one has to perform exact diagonalizations of huge matrices (e.g., Hubbard-like matrices) for investigating the BZ with the aid of finite-sized systems having a very small number of sites.
Contributed by: Jessica Alfonsi (University of Padova, Italy) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Brillouin zone (BZ) sampling with a four-site chain and  can also be achieved with a two-site chain and
can also be achieved with a two-site chain and  for the
for the  points at the center and at the edge of the BZ and with
points at the center and at the edge of the BZ and with  for the
for the  points at
points at 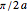 .
.
R. Jullien and R. M. Martin, "Ground-State and Low-Lying Excitations of the Periodic Anderson Hamiltonian in One Dimension from Finite-Cell Calculations," Physical Review B 26(11), pp. 6173-6185, Section III: Methods. A. "The modified periodic boundary conditions," 1982.
J. Alfonsi, "Small Crystal Models for the Electronic Properties of Carbon Nanotubes," Ph.D. thesis, University of Padova, 2009, Chapters 4 and 6, and references therein.
Permanent Citation