Wannier Representation for Tight-Binding Hamiltonian of a Periodic Chain with N Sites

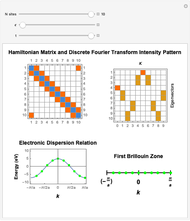
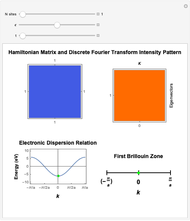
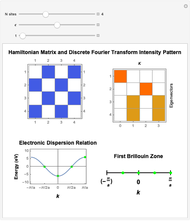
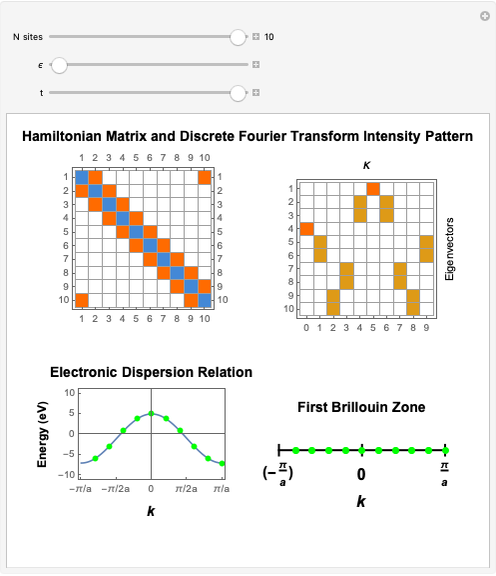
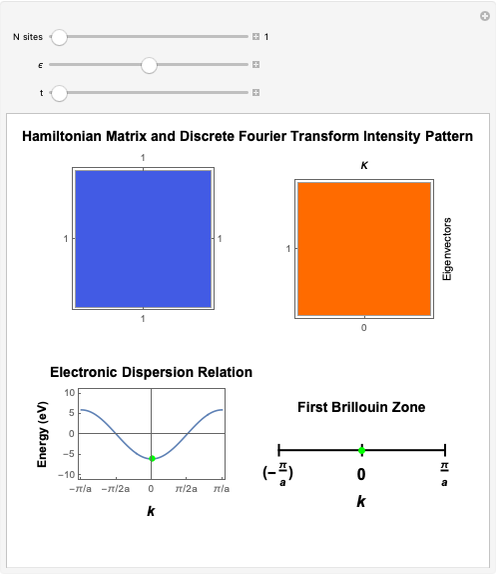
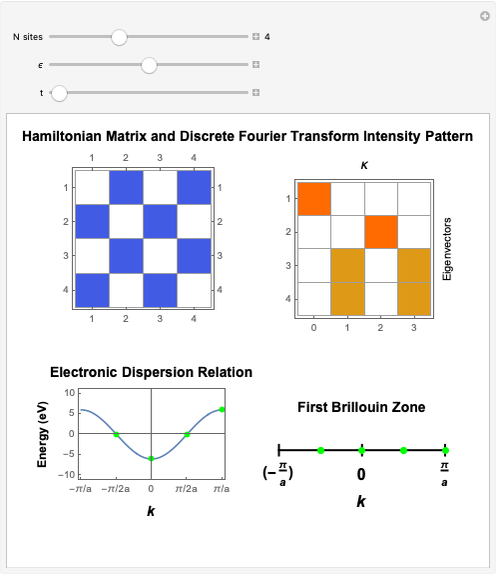
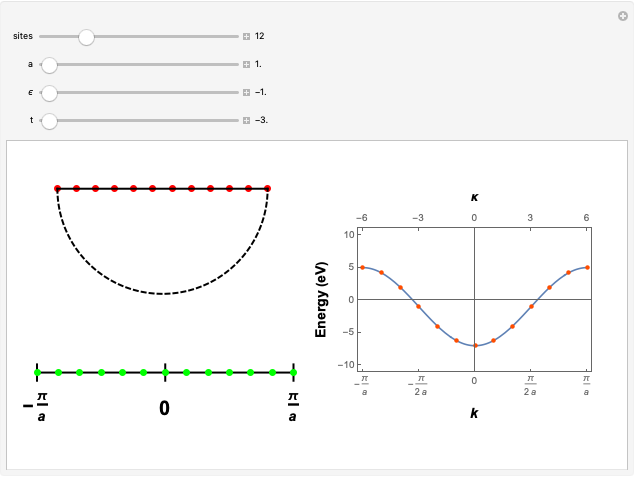
This Demonstration shows the construction of the tight-binding Hamiltonian matrix for a periodic chain with sites within the Wannier representation. The Hamiltonian in second quantization form is given by 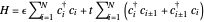, where 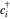and 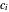are the fermionic creation and destruction operators of electrons at each site , respectively. Periodic boundary conditions at chain ends are expressed as and 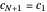. The tight-binding on-site energy parameter ϵ gives the on-diagonal matrix elements, the hopping parameter gives the off-diagonal matrix elements. Both 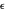and 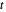are expressed in electron-volts. This representation, unlike the reciprocal space-based Bloch representation, works in real space. 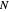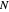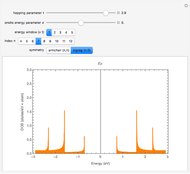However, physically, it is fully equivalent, since with sites one can sample -points in the reciprocal space of the first Brillouin zone (BZ). Thus the same energy eigenvalues are expected from exact diagonalization of the Hamiltonian matrix. 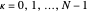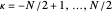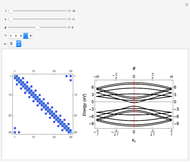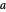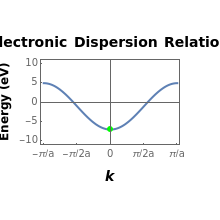The information about the quantum numbers ( or equivalently in the reduced BZ scheme) and the related -points ( with lattice parameter of the chain) can be extracted by performing a discrete Fourier transform on each of the obtained eigenvectors and subsequently by inspecting the frequency components with nonzero intensity. The electronic energy eigenvalues associated to the -points thus obtained are plotted and superimposed onto the analytical Bloch dispersion relation 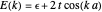in order to show the full equivalence of the Wannier result with the one for the reciprocal space.