Brillouin Zone of a 2D Square Lattice: Tight Binding Approximation

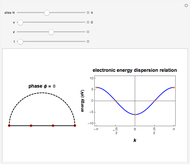
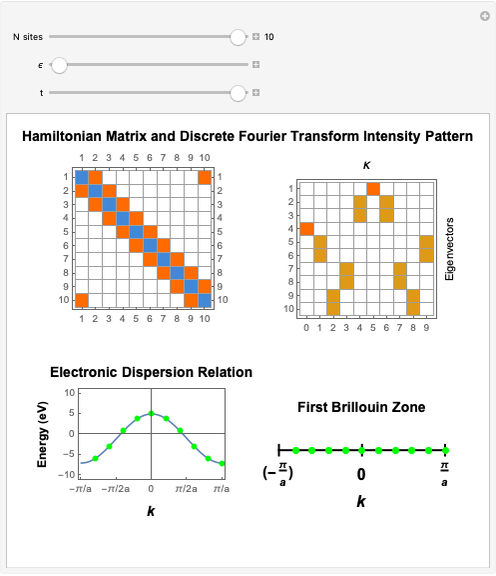
The energy structure of crystals depends on the interactions between orbitals in the lattice. The tight binding approximation (TB) neglects interactions between atoms separated by large distances, an approximation which greatly simplifies the analysis. In solid-state physics, the TB model calculates the electronic band structure using an approximate set of wave functions based upon superposition of orbitals located at each individual atomic site.

In a TB approximation including only first nearest neighbor s-orbital, the band structure, i.e. the electron energy dispersion in the Brillouin zone of the crystal, is given by

(1)

where 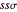is the overlap integral between s-orbitals, is the translation vector of the lattice, and 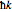is the "crystal momentum"—the quantum number for periodic systems. The band structure for a simple cubic lattice can now be readily calculated. Assuming that the bond integrals couple only to the first four nearest neighbors with position vectors equal to 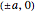and , (1) gives

.

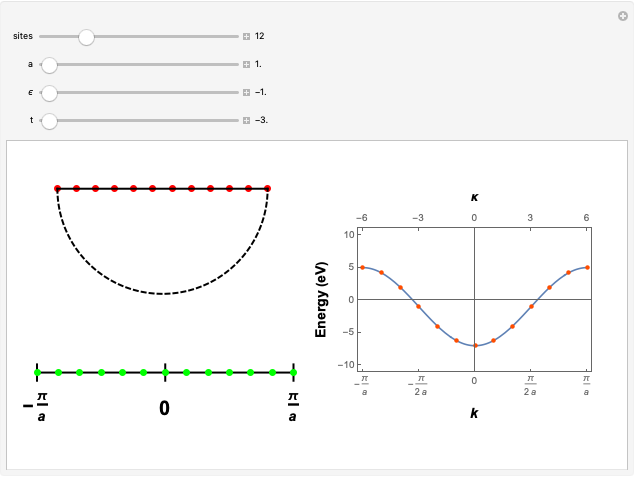
(a)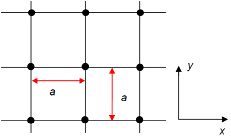

(b)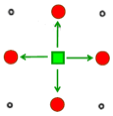

(c)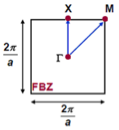

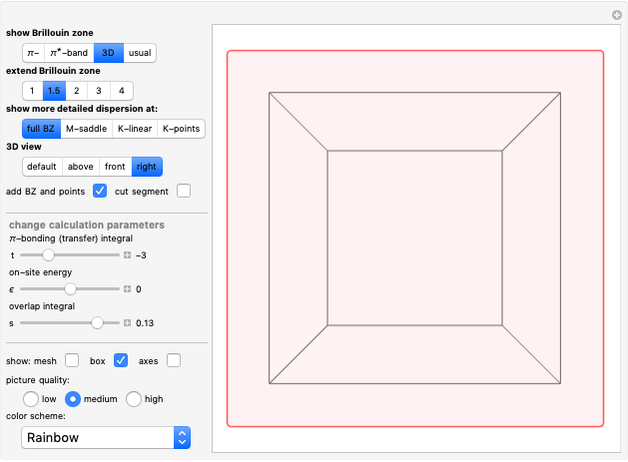
Figure: (a) lattice fragment; (b) four first nearest neighbors included in transfer; (c) the first Brillouin zone.

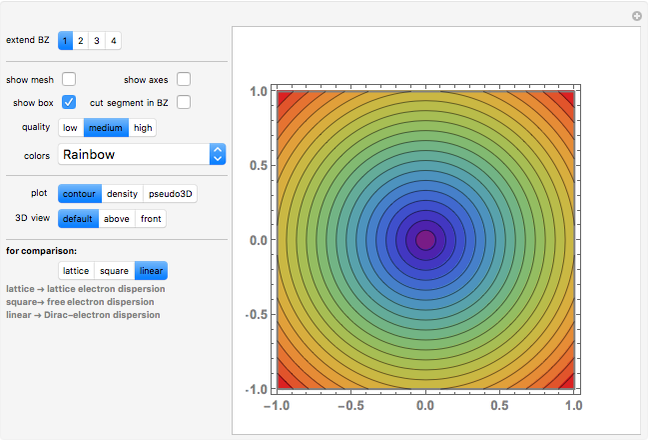
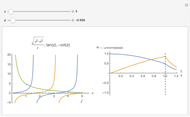
Setter bars let you compare the lattice electron behavior with the parabolic dispersion curves of the free electrons in free space,

,

and with the linear dispersion curves of Dirac electrons (as in graphene -points),

.

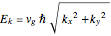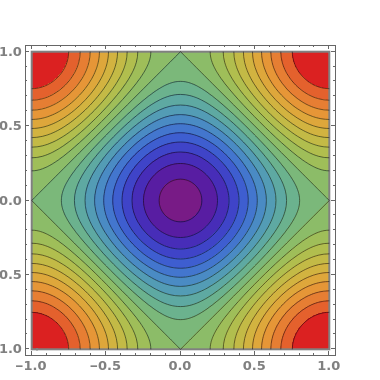
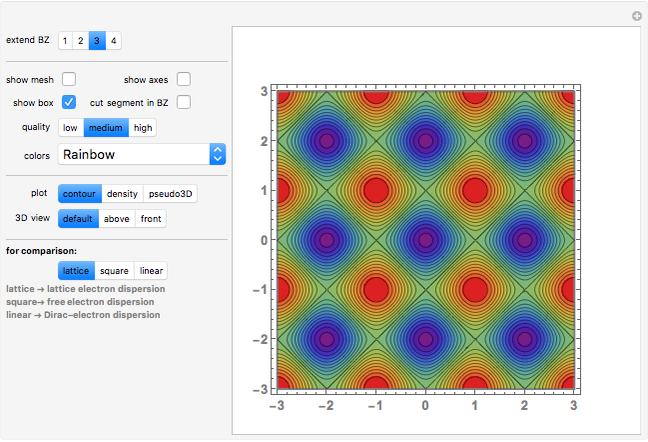
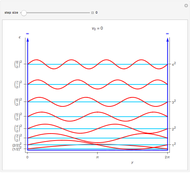
Snapshot 1: constant energy contours for the -band in the first Brillouin zone of a 2D one-base simple square lattice

Snapshot 2: constant energy contours for the free Dirac electrons in free space

Snapshot 3: constant energy contours for the 2D square lattice in an extended 3×3 Brillouin zone

Snapshot 4: energy dispersion for the -band in an extended 3×3 Brillouin zone of a 2D square lattice

Snapshots 5 and 6: same energy dispersion viewed from top and front

References:

D. G. Pettifor, Bonding and Structure of Molecules and Solids, Oxford: Clarendon Press, 1995.

C. Kittel, Solid State Physics, Hoboken, NJ: John Wiley & Sons, Inc., 1996.