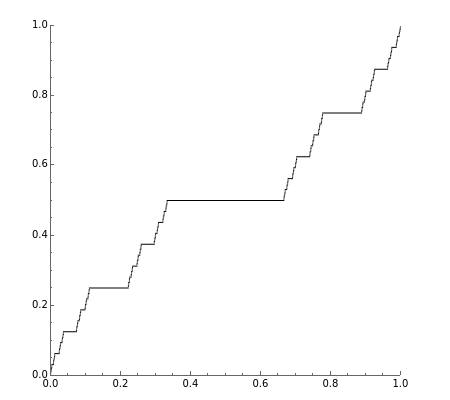
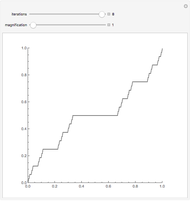
Cantor Function

Initializing live version

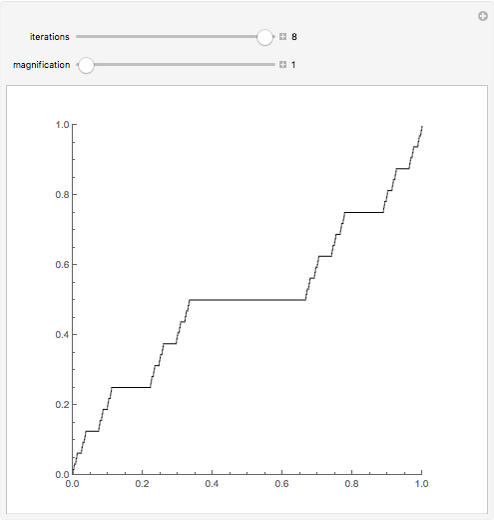
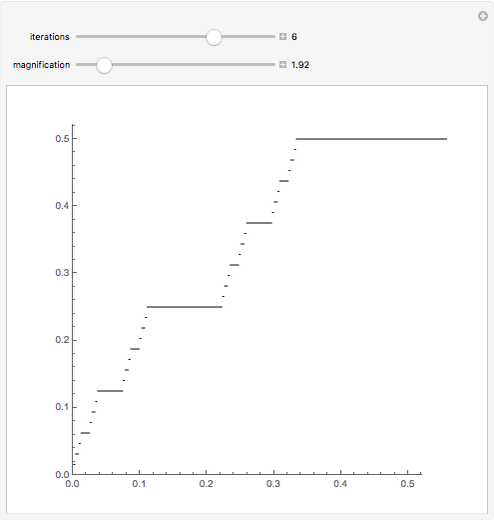
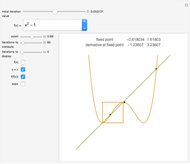
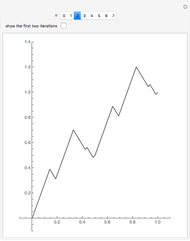
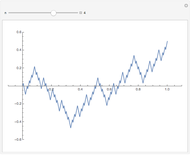
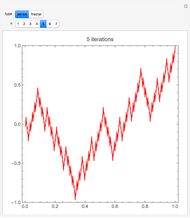
This Demonstration runs eight iterations of the Cantor function. You can zoom in close to the origin to see the fractal nature of the function.

Contributed by: Douglas Rivers (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Program segment borrowed from M. Trott's The Mathematica Guidebook for Graphics, New York: Springer-Verlag, 2004.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send