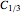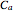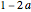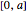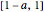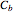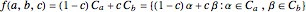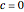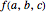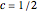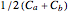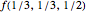The Cantor set has many interesting and initially unintuitive properties: it is a fractal, perfect, nowhere-dense, totally disconnected, closed set of measure zero. Yet two such sets can be combined to give a simple interval.
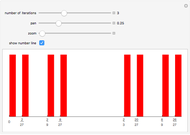
The (standard) Cantor set 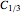 is the limit of the following iteration. Starting with an interval, take out its middle third, leaving two closed intervals at each end. Repeat on each subinterval; then continue to any depth, doubling the number of intervals each time.
is the limit of the following iteration. Starting with an interval, take out its middle third, leaving two closed intervals at each end. Repeat on each subinterval; then continue to any depth, doubling the number of intervals each time.
This can be generalized to 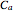 by taking out the fraction
by taking out the fraction 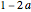 at each stage; this leaves the intervals
at each stage; this leaves the intervals 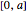 and
and 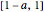 at the first stage. (Other generalizations are to take out the second and fourth fifths at each stage, etc., or to use a sequence of fractions, but not here.)
at the first stage. (Other generalizations are to take out the second and fourth fifths at each stage, etc., or to use a sequence of fractions, but not here.)
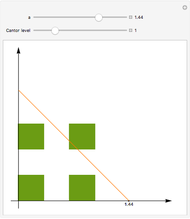
Two Cantor sets 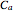 and
and 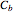 using the fractions
using the fractions  and
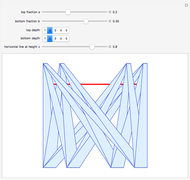
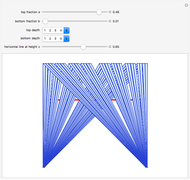
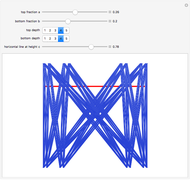
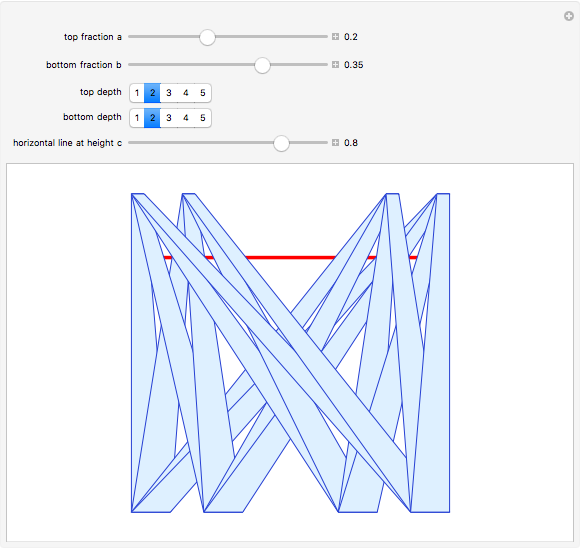
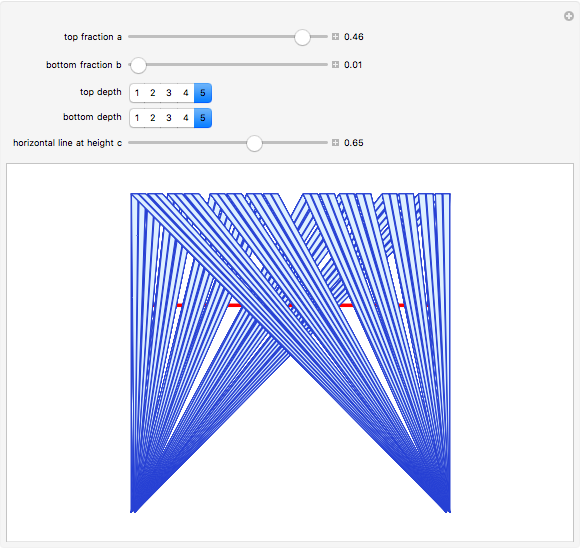
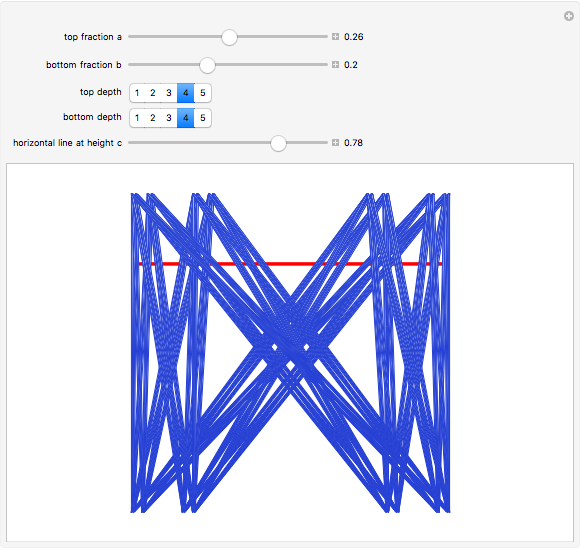
and  are constructed one unit apart. All of the points of
are constructed one unit apart. All of the points of 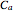 are joined to all of the points of
are joined to all of the points of 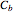 by lines; these sets of lines are approximated by overlapping bands (parallelograms) that get thinner and more numerous as the depth increases.
by lines; these sets of lines are approximated by overlapping bands (parallelograms) that get thinner and more numerous as the depth increases.
The cross-section of the bands by the horizontal line  give approximations to the set
give approximations to the set 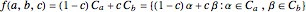 , which is
, which is 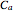 for
for 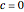 and
and 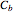 for
for  . So this set
. So this set 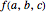 is a kind of blend of
is a kind of blend of 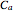 and
and 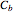 or a convex interpolation between
or a convex interpolation between 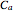 and
and 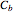 . For
. For 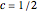 ,
, 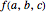 is
is 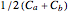 , the average of the two sets, or its scaled sum.
, the average of the two sets, or its scaled sum.
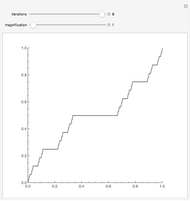
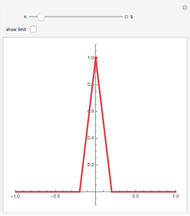
What is the nature of 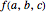 ? As you can see here (or in the Demonstration The Sum of Two Cantor Sets),
? As you can see here (or in the Demonstration The Sum of Two Cantor Sets), 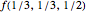 is the whole unit interval. If
is the whole unit interval. If 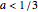 or
or 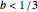 , then
, then 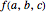 appears to be fractal.
appears to be fractal.
[less]