Cellular Automaton Compressibility

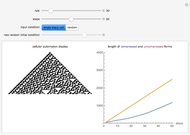
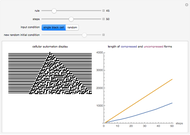
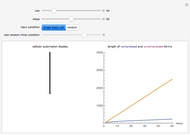
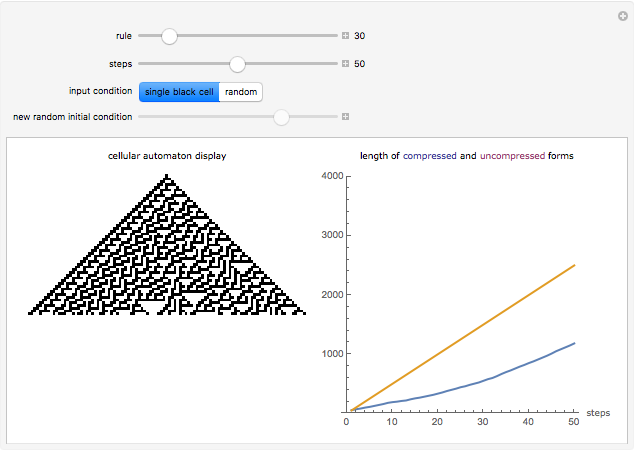
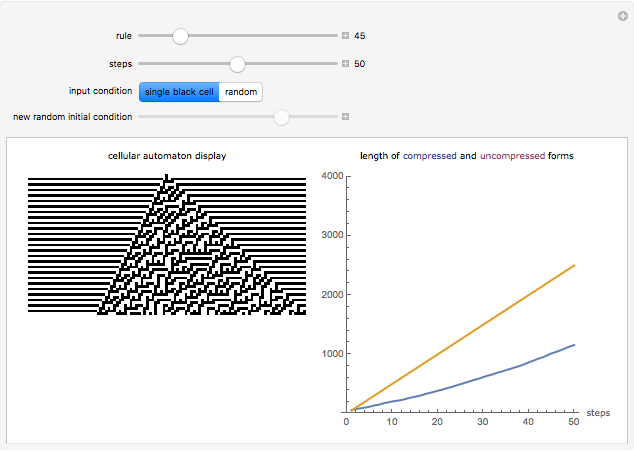
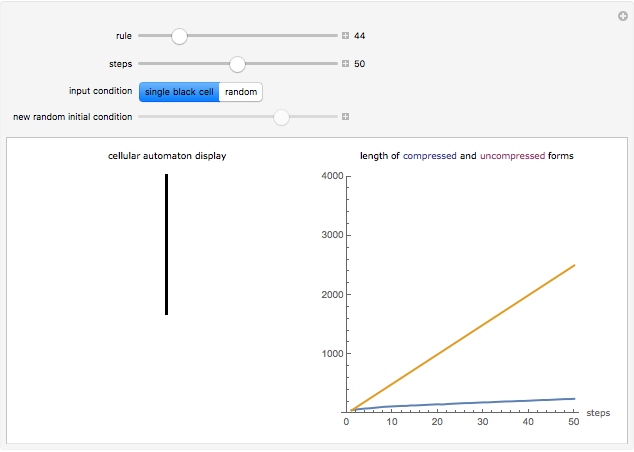
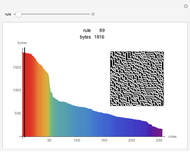
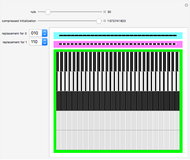
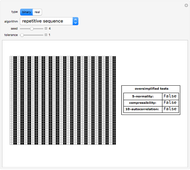
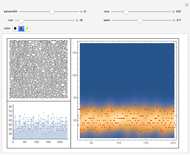
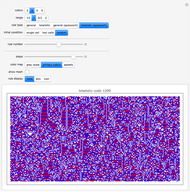
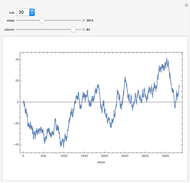
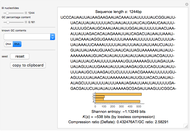
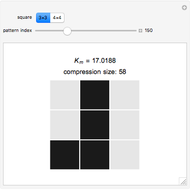
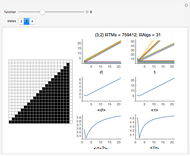
The difference in length between the compressed and uncompressed forms of the output of a cellular automaton is a good approximation of its algorithmic complexity. For most cases, the length of the compressed form levels off, indicating that the cellular automaton output is repetitive and can easily be described. However, in cases like rules 30, 45, 110, or 73, the length of the compressed form grows rapidly, corresponding to the apparent randomness and lack of structure in the display.