Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Chaos in a Plant Pathogen/Hyperparasite Population Model

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

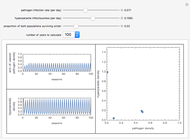
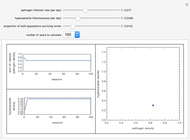
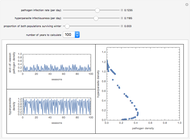
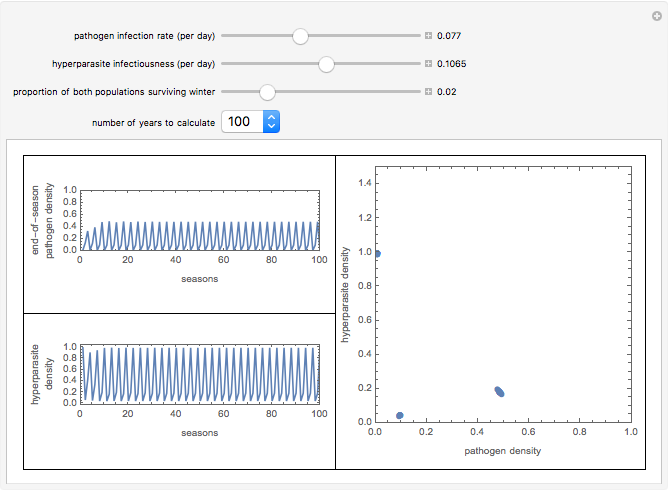
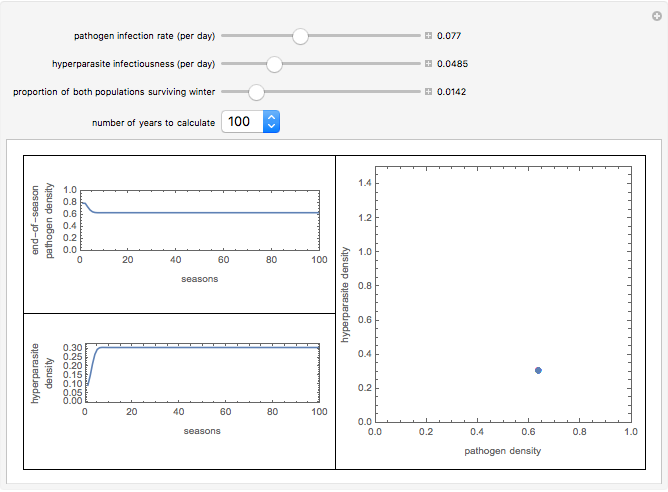
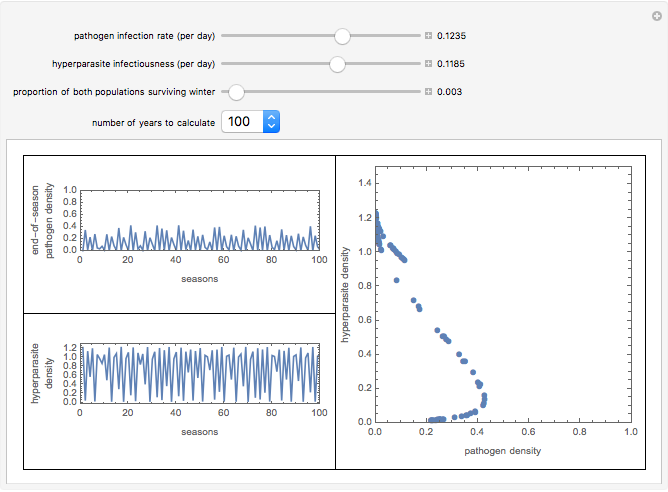
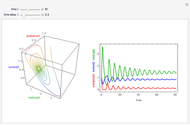
This Demonstration shows successive end-of-season populations of a plant pathogen population increasing in conditions that become progressively unfavorable during the season, and which is limited by the plant population available. A hyperparasite population increases on the pathogen faster if there is more pathogen present. Annually BOTH populations are reduced to a fraction of themselves by the off-season, when the host plant is absent and the weather is unfavorable.

[more]

The graphic shows time series for each component and a phase-plane plot for the final 50% of the time series. The pattern varies from a stable population at the end of each year through a variety of cycles to a chaotic fluctuation.

[less]

Contributed by: Michael Shaw (June 2012)
Open content licensed under CC BY-NC-SA

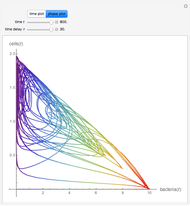
Snapshots

Details

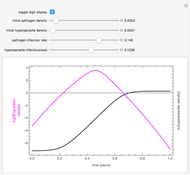
Within a season, the plant pathogen increases at a per capita rate that is reduced in proportion to the population size and decreases during the season as conditions become progressively unfavorable. It is destroyed by a hyperparasite at a rate that is proportional to both populations. The parasite harms the host but has no in-season death rate. This models something with long-lived structures but only one food source. If the pathogen population as a proportion of its maximum is , and the population of the hyperparasite is , where both are functions of time running from 0 to 1 within season 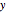, the equations are

,

,

, .

Between seasons, both populations are reduced to a small fraction of their end-of-season sizes:

,

.

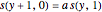References

[1] M. W. Shaw, "The Population Dynamical Consequences of Density-Dependence in Fungal Plant Pathogens," in Stress in Yeast and Filamentous Fungi (S. A. Avery, M. Stratford, and P. van West, eds.), British Mycological Society Symposia Series, 27, Dordrecht: Kluwer, 2008 pp. 53–66.

M. W. Shaw, "Seasonally Induced Chaotic Dynamics and Their Implications in Models of Plant Disease," Plant Pathology 43(5), 1994 pp. 790–801.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send