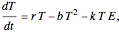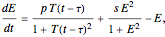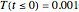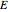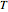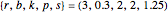Chaos Induced by Delay in Model of the Immune Response

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
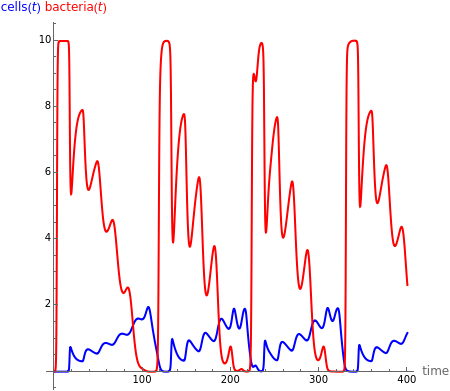
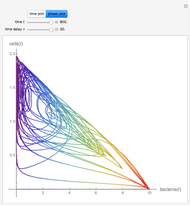
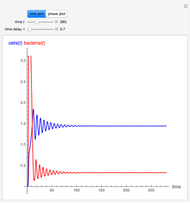
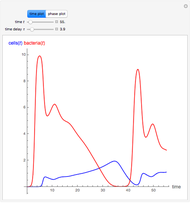
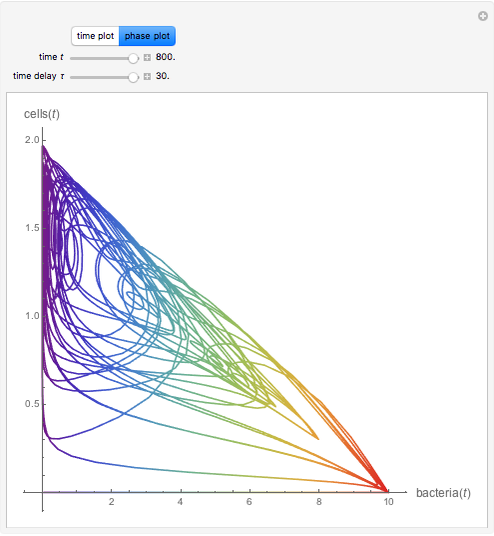
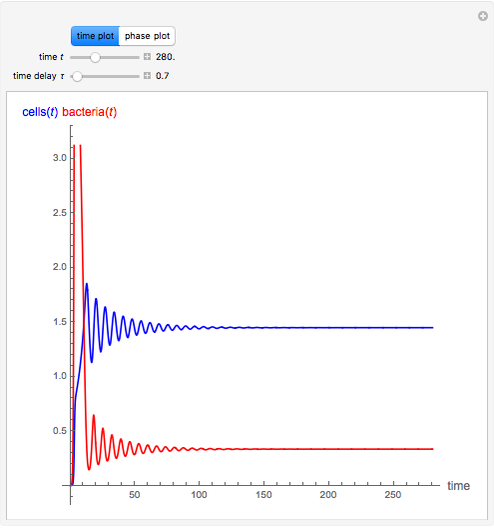
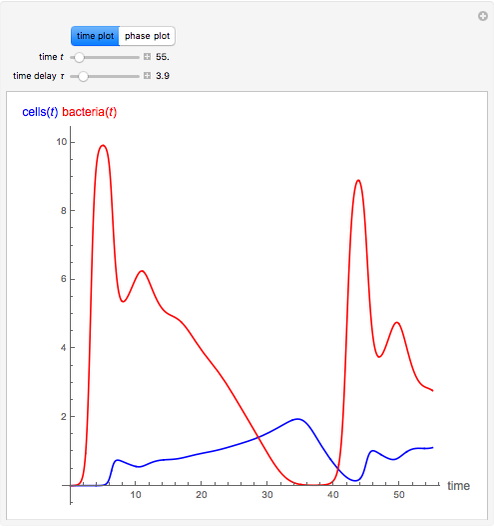
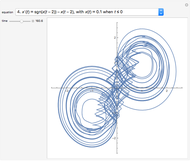
This Demonstration shows the effect of time delay in a basic model of the immune system.
[more]
Contributed by: Clay Gruesbeck (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] E. de Souza, M. Lyra, and I. Gleria, "Critical Behavior of the Delay-Induced Chaos Transition in a Nonlinear Model of the Immune Response," Brazilian Journal of Physics, 39(2A), 2009 pp. 431–434. doi:10.1590/S0103-97332009000400015.
[2] H. Mayer, K. S. Zaenker, and U. an der Heiden, "A Basic Mathematical Model of the Immune Response," Chaos, 5(1), 1995 pp. 155–161. doi:10.1063/1.166098.
Permanent Citation