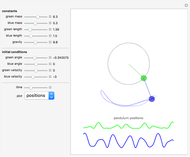
Chaotic Motion of a Damped Driven Pendulum: Bifurcation, Poincaré Map, Power Spectrum, and Phase Portrait

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A continuous time system with a minimum of three independent dynamic variables can exhibit chaotic motion under certain initial conditions. A damped and driven pendulum is one of the simplest systems to use in the study of chaos. A defining characteristic of a chaotic system is its extreme sensitivity to initial conditions. This Demonstration implements a number of methods used in the analysis of such systems: bifurcation plots, Poincaré maps, phase portraits, time series, and power spectra. The Lyapunov exponent method will be included in a future version.
[more]
Contributed by: Nasser M. Abbasi (October 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Theory background: 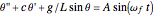 is a second-order nonlinear differential equation that models the motion of a simple pendulum subject to a forcing function
is a second-order nonlinear differential equation that models the motion of a simple pendulum subject to a forcing function  , where
, where  is the damping coefficient,
is the damping coefficient, 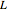 is the length of the pendulum, and
is the length of the pendulum, and  is its angular position.
is its angular position.
For ease of analysis, this differential equation is first converted to a nondimensional form by defining 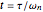 ,
, 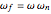 ,
, 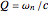 , and
, and 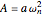 , where
, where  is the pendulum's undamped natural frequency given by
is the pendulum's undamped natural frequency given by 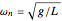 and
and  is the gravitational constant.
is the gravitational constant.
Applying this transformation results in 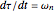 , and using
, and using  results in
results in 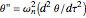 ,
,  , and
, and 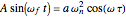 . Substituting these back into the original differential equation and dividing throughout by
. Substituting these back into the original differential equation and dividing throughout by 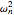 gives
gives 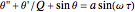 , where the derivatives are now with respect to
, where the derivatives are now with respect to  .
. 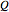 is called the quality factor. This is the nonlinear differential equation that is used in this Demonstration, not the original one.
is called the quality factor. This is the nonlinear differential equation that is used in this Demonstration, not the original one.
The driver frequency  is given by
is given by 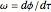 , where
, where  is the phase angle. This system is now converted to matrix form
is the phase angle. This system is now converted to matrix form 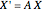 , which contains three first-order differential equations as follows. Let
, which contains three first-order differential equations as follows. Let  ,
, 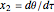 , and
, and 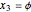 . Taking derivatives gives
. Taking derivatives gives  ,
, 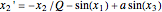 , and
, and 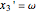 . The system in state can thus be written
. The system in state can thus be written 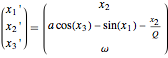 .
.
The Mathematica built-in function NDSolve[] is now used for this system. The initial conditions are 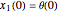 ,
,  , and
, and  . Therefore, the three dynamic variables (or state-space variables) in this model are
. Therefore, the three dynamic variables (or state-space variables) in this model are 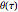 ,
, 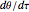 , and
, and 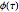 .
.
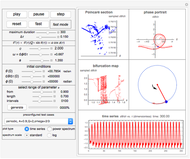
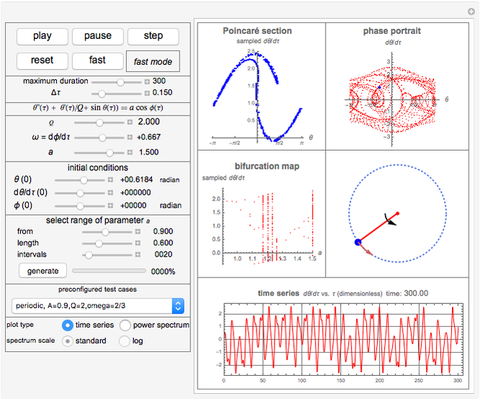
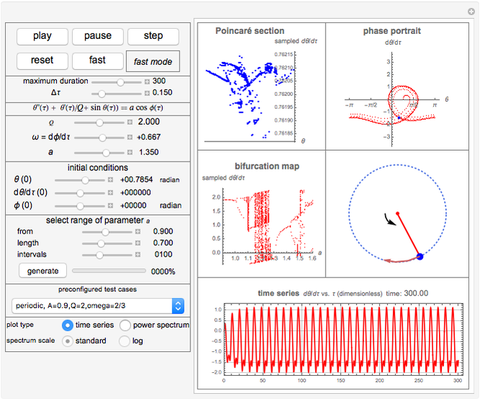
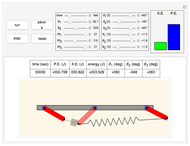
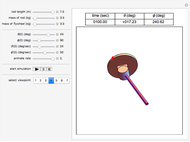
This describes how to use the Demonstration: The top buttons are used to run and control the simulation. You can vary the simulation time up to a maximum of 500 units. Use the "pause" button to pause the simulation at any time. Use the "step" button to advance the time by one unit. Use the "reset" button to bring the system back to initial time. Use the button labeled "fast" to advance the system to the end of the simulation period immediately without going through the animation steps. Use the slider labeled "Δτ" to adjust the size of the time step. The smaller the step size, the more accurate and smoother the motion will appear, but it will take a longer time to run.
The parameters of the system 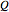 ,
,  , and
, and  are varied using the sliders. Making
are varied using the sliders. Making 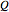 zero will remove damping from the system, while making
zero will remove damping from the system, while making  zero will remove the forcing function. This effectively makes the system run as a standard simple pendulum with no damping and no forcing function.
zero will remove the forcing function. This effectively makes the system run as a standard simple pendulum with no damping and no forcing function.
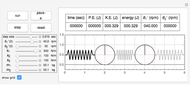
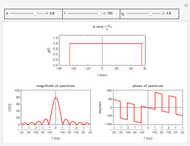
There are five main plots on the display. The Poincaré map is always plotted to reflect the state at the end of the simulation period. The 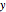 axis represents the values of the angular velocity of the pendulum sampled at time intervals equal in magnitude to the period of the forcing function. The phase plot is updated as time is advanced and at each step, and similarly for the time series plot and the power spectrum plot.
axis represents the values of the angular velocity of the pendulum sampled at time intervals equal in magnitude to the period of the forcing function. The phase plot is updated as time is advanced and at each step, and similarly for the time series plot and the power spectrum plot.
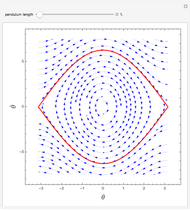
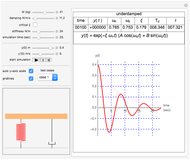
Switch between the time series plot and the power spectrum plot using the option selection shown in the left part of the display. The phase portrait was drawn such that the angle of the pendulum is kept between 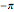 and
and  to make it easier to draw the plot.
to make it easier to draw the plot.
The display of the actual physical pendulum is also shown with a small arrow attached to the bob. The length of the arrow indicates the relative magnitude of the current angular velocity. The inner arrow represents the relative strength of the external torque. The directions of the arrows represent the sign of the respective values. An anticlockwise arrow direction indicates a positive sign.
The bifurcation plot is only updated when you click the button labeled "generate". This lets you choose your parameters before viewing the final result, as it takes time to generate the plot. The parameters used to select the bifurcation plot let you select the range of values of the parameter  (the torque amplitude). The more intervals you ask for, the clearer the plot will be, but it takes longer to generate as the system is numerically solved for each interval. Sampling of values starts after the time has reached 150 periods of the driver frequency, in order to allow transient effects to attenuate sufficiently. The solution is then run for an additional 100 periods to collect the data for the plot. This is done at each interval. Therefore, the
(the torque amplitude). The more intervals you ask for, the clearer the plot will be, but it takes longer to generate as the system is numerically solved for each interval. Sampling of values starts after the time has reached 150 periods of the driver frequency, in order to allow transient effects to attenuate sufficiently. The solution is then run for an additional 100 periods to collect the data for the plot. This is done at each interval. Therefore, the 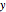 axis for the bifurcation is similar to the
axis for the bifurcation is similar to the 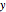 axis of the Poincaré map; however, the
axis of the Poincaré map; however, the  axis represents
axis represents  and not
and not  as in the phase portrait and Poincaré map.
as in the phase portrait and Poincaré map.
The current time for the simulation is displayed on the right side of the title of the bottom plot. When the system reaches the end of the simulation, the "reset" button can be used bring it back to the initial time. The simulation will not advance beyond 500 time units.
The Demonstration comes with a number of test cases preconfigured to show different aspect of the behavior of the system. These test cases are selected from the popup menu at the top right. Once a test case is selected, the user interface parameters are updated automatically, and the final simulation result is shown based on the use of these new parameters.
Possible issues:
1. The maximum simulation duration of 500 was fixed in the program for efficient implementation. Hence this value should not be increased without adjusting the corresponding internal variable in the software that depends on this value.
2. When the current time is at the maximum duration time, clicking the "run" or "step" button has no effect. The "reset" button can be used to bring the system to the initial state in order to run a new simulation.
References
[1] R. Fitzpatrick. "Introduction to Computational Physics." (2006) http://farside.ph.utexas.edu/teaching/329/lectures/node47.html.
[2] R. Gilmore and C. Letellier, The Symmetry of Chaos, Oxford: Oxford University Press, 2007.
[3] C. Greene. "Driven Pendulum." (2000) http://www.phy.davidson.edu/StuHome/chgreene/chaos/Pendulum/pendulum_content_frame.htm.
[4] G. Leo. "Chaotic Dynamics of a Damped, Driven Pendulum." (2007) http://homepage.ntlworld.com/gerry.leo/Theory.html.
Permanent Citation