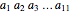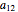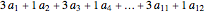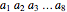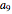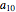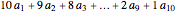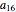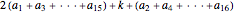Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Check Digit Schemes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

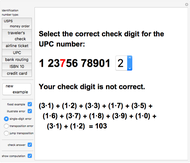
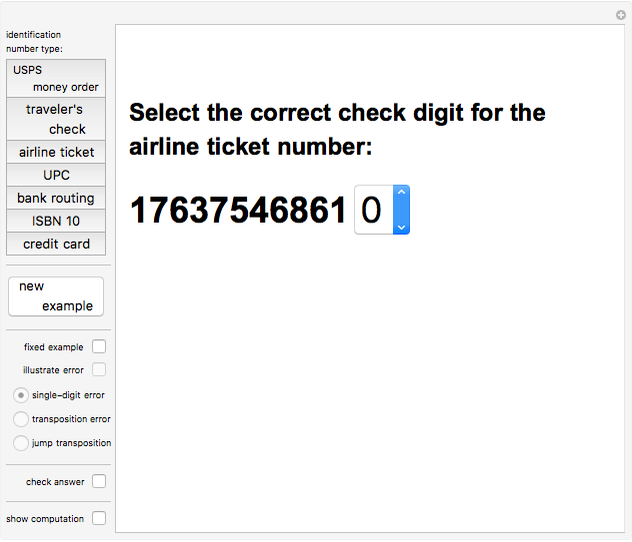
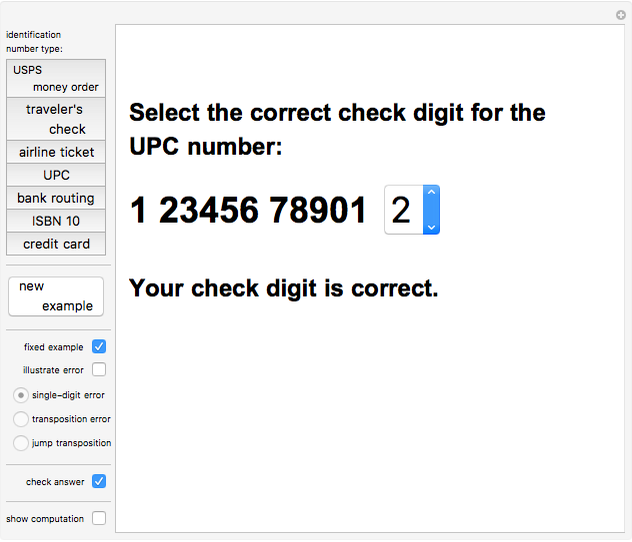
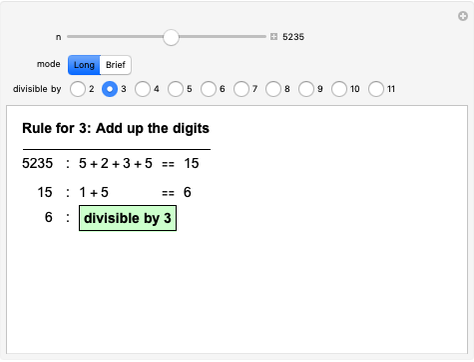
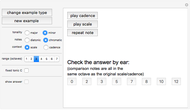
Identification numbers often have a check digit appended to them in order to help catch copy and transmission errors. Seven common check digit schemes are illustrated here. The "new example" button gives a random identification number of the desired type. Use the popup menu to select the check digit, then check your answer. If your answer is incorrect, you can view the appropriate computation and try again. The "fixed example" and "illustrate error" options show several of the most common errors and allow you to explore whether a given check digit scheme will catch such errors.

[more]

The United States Postal Service money order check digit scheme requires that the check digit (the 11th digit) be the remainder upon division by 9 of the sum of the first 10 digits of the identification number.

The traveler's check scheme requires that the check digit be chosen so that the sum of all 10 digits (including the check digit) is divisible by 9.

In the airline ticket scheme, the check digit (the 12th digit), is the remainder upon division by 7 of the 11-digit identification number.

Given a UPC number , the check digit is chosen so that the weighted sum is divisible by 10.

Given a bank routing number , the check digit is the remainder upon division by 10 of the weighted sum .

For a 10-digit ISBN number with the first nine digits , the check digit is chosen so that the weighted sum has a remainder of 0 upon division by 11. The symbol X is used if the check digit must equal 10.

The credit card check digit is computed so that is divisible by 10. The number is the number of digits in the odd-numbered positions whose value exceeds 4.

[less]

Contributed by: Marc Brodie (July 2011)
(Wheeling Jesuit University)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] COMAP, For All Practical Purposes, New York: W. H. Freeman and Company, 2009.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send