Visible Divisibility Tests

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
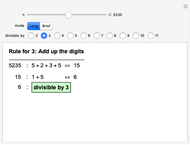
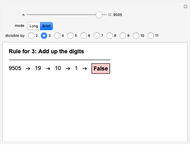
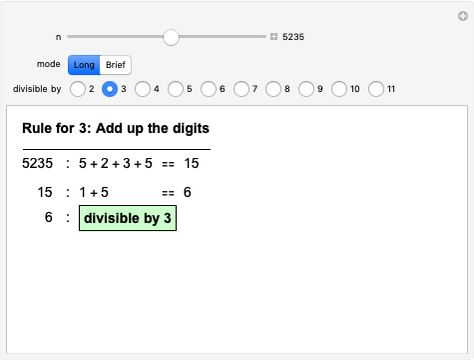
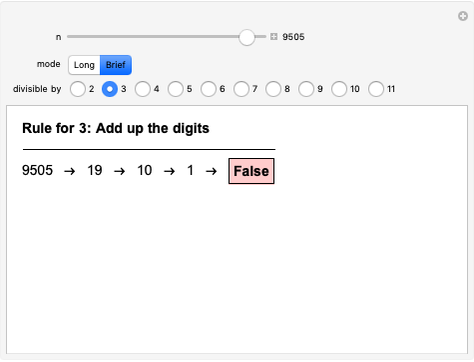
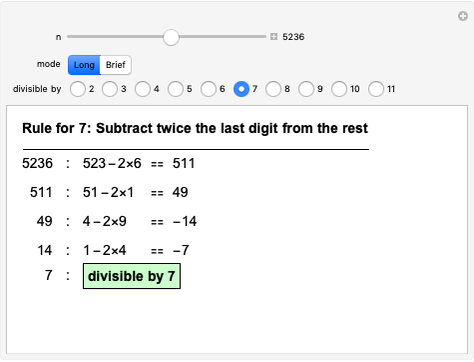
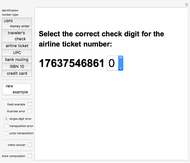
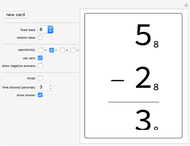
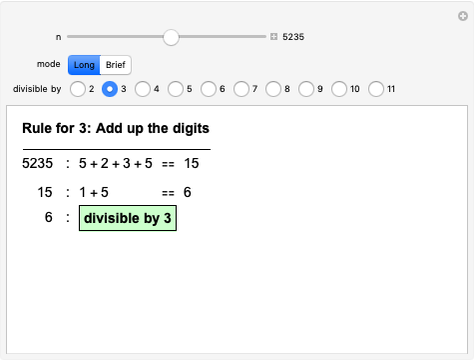
Most people are familiar with the test for divisibility by 3: add up all the digits and check whether the result (the digit sum) is divisible by 3. Other divisibility tests are less well known, such as alternately adding and subtracting digits to test for divisibility by 11. This Demonstration implements divisibility tests for dividing by 2, 3, …, 11. In all cases the rule is given and a step-by-step application shown, either in "Long" or "Brief" form. The radio buttons choose which test to apply and the slider selects the number to test. (Clicking the "+" sign by the slider opens another panel where numbers can be entered directly or incremented/decremented.)
Contributed by: Kenneth E. Caviness (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
There are other available divisibility tests in the literature; see the MathWorld link below for a good introduction. The immediate impetus to create this Demonstration came from a rereading of Paul M. Cohen's short article "Divisibility Tests Remembered," Focus, 23(8), 2003 p. 8. I am indebted to him for the "Brief" notation used in this Demonstration and for reminding me of the fascination of these techniques.
Note: In some of these implementations it is possible to arrive at a negative number in the course of the iteration, and so I have always taken the absolute value of the results where this is a possibility. In a similar vein, the value produced by the divisibility by 6 algorithm is actually the negative of that found by the algorithm described on the MathWorld page, but it seemed easier to do it mentally this way, and we are taking the absolute value so we are free to use either one. (Caution: This means that  is not necessarily equal to
is not necessarily equal to  , but the remainder was not preserved by the 7-rule anyway, so the loss is not great. Whether the remainder is zero or not is preserved.)
, but the remainder was not preserved by the 7-rule anyway, so the loss is not great. Whether the remainder is zero or not is preserved.)
Permanent Citation