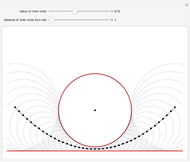
Cissoid of Diocles

Initializing live version

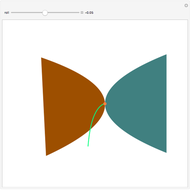
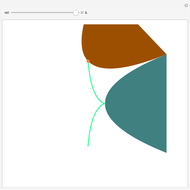
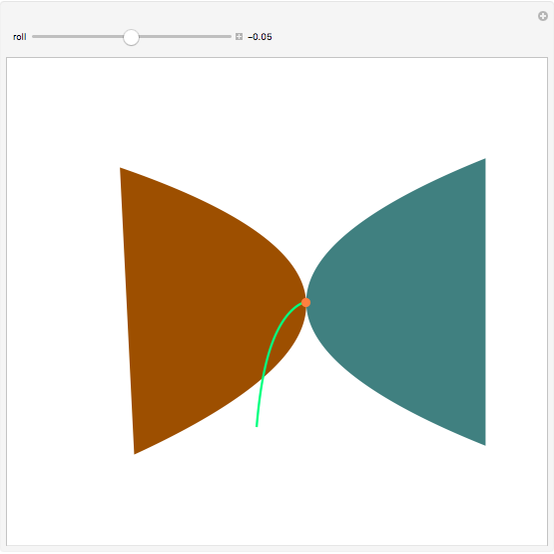
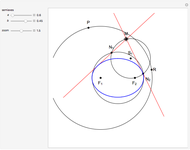
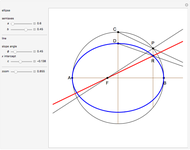
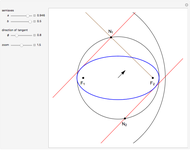
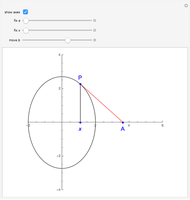
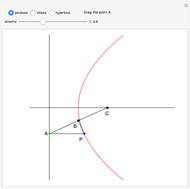
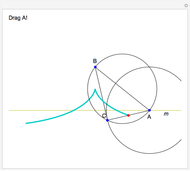
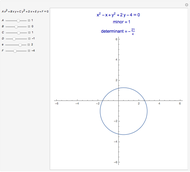
The cissoid of Diocles can be considered as the locus of the vertex of one parabola rolling on an equal parabola.

Contributed by: Izidor Hafner (August 2012)
Open content licensed under CC BY-NC-SA

Snapshots

detailSectionParagraph


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send