Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Collinearity of an Orthocenter, the Incenter, and the Circumcenter

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

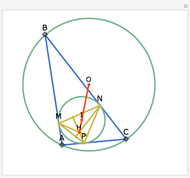
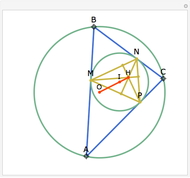
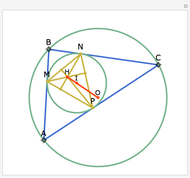
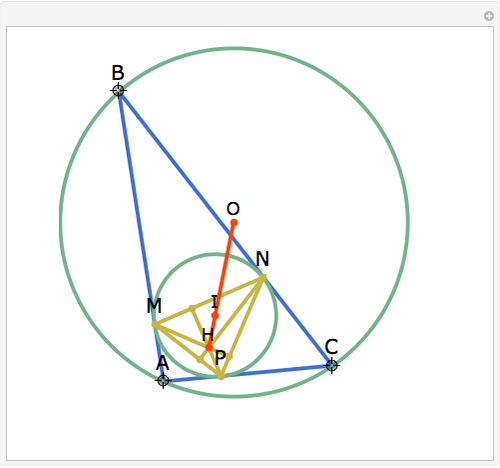
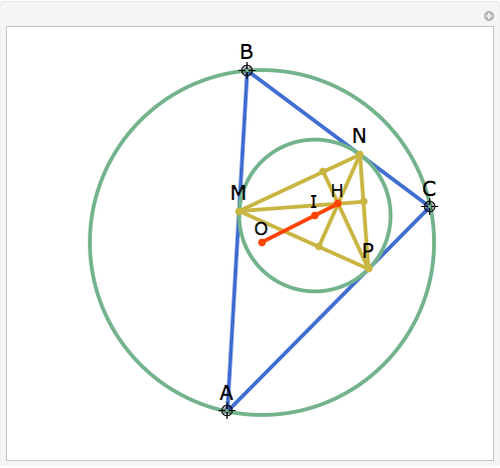
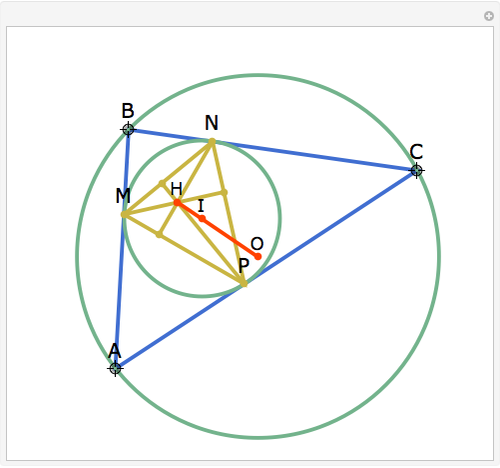
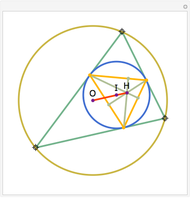
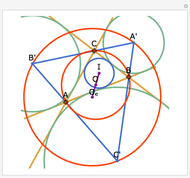
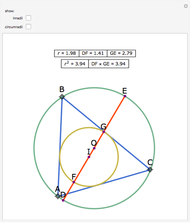
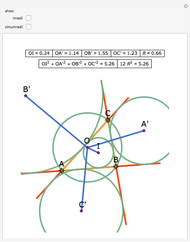
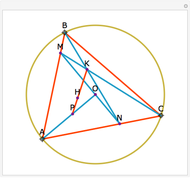
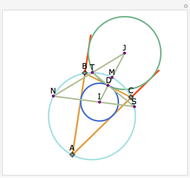
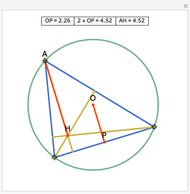
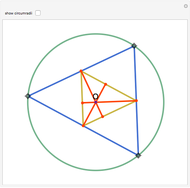
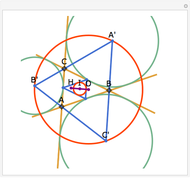
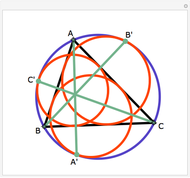
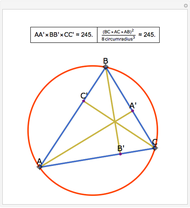
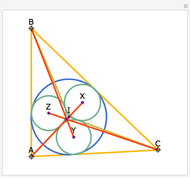
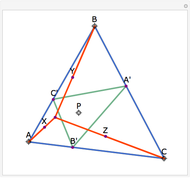
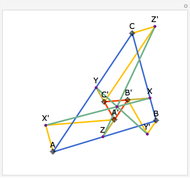
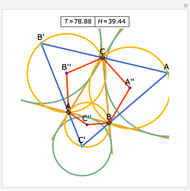
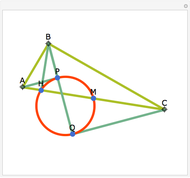
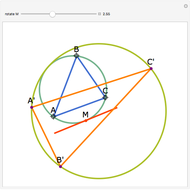
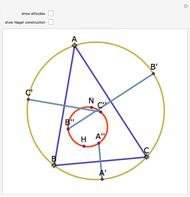
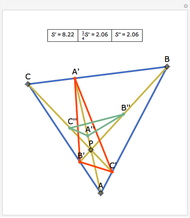
Let ABC be a triangle with incenter I and circumcenter O. Let the incircle intersect AB, BC, and CA at M, N, and P, respectively. Let the orthocenter (the intersection of the altitudes) of MNP be H. Then H, I, and O are collinear.

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

See Example 6 on page 4 of Mathematical Excalibur, Volume 9, No. 2.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send