A Concurrency of Lines through Points of Tangency with Excircles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
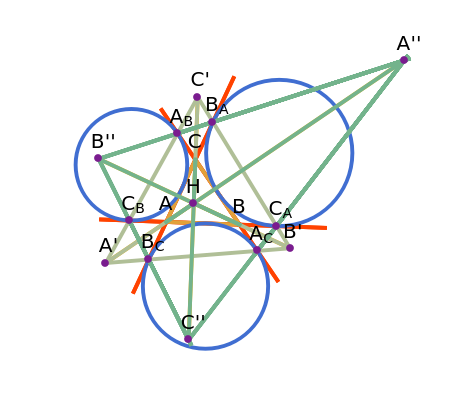
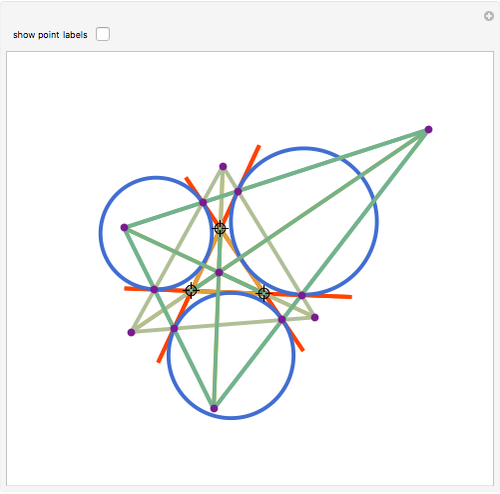
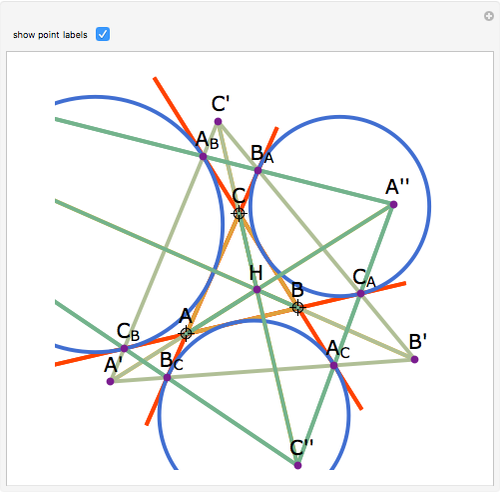
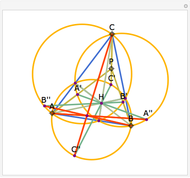
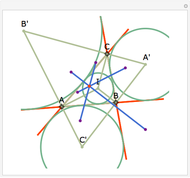
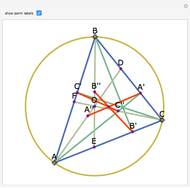
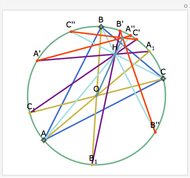
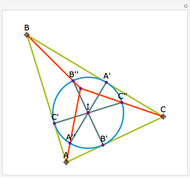
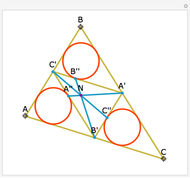
Let ABC be a triangle with orthocenter H. Let 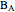 be the point of tangency of CA with the excircle opposite A, and similarly define
be the point of tangency of CA with the excircle opposite A, and similarly define 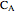 ,
, 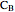 ,
, 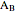 ,
, 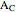 , and
, and 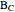 . Let
. Let 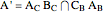 ,
, 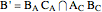 , and
, and 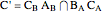 . Let
. Let 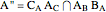 ,
, 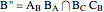 , and
, and  . Then AA', BB', and CC' as well as AA'', BB'', and CC'' meet at H.
. Then AA', BB', and CC' as well as AA'', BB'', and CC'' meet at H.
Contributed by: Jay Warendorff (September 2008)
After work by: Paul Yiu
Open content licensed under CC BY-NC-SA
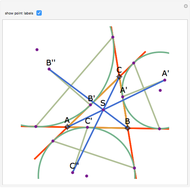
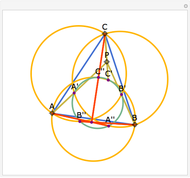
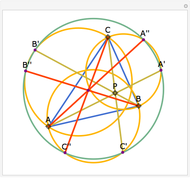
Snapshots
Details
See the paper "Synthetic proof of Paul Yiu's excircles theorem" available on Darij Grinberg's home page.
Permanent Citation
"A Concurrency of Lines through Points of Tangency with Excircles"
http://demonstrations.wolfram.com/AConcurrencyOfLinesThroughPointsOfTangencyWithExcircles/
Wolfram Demonstrations Project
Published: September 24 2008