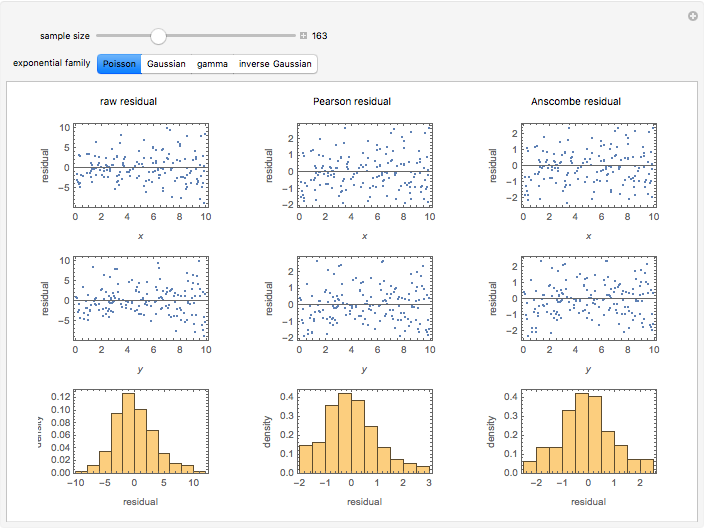
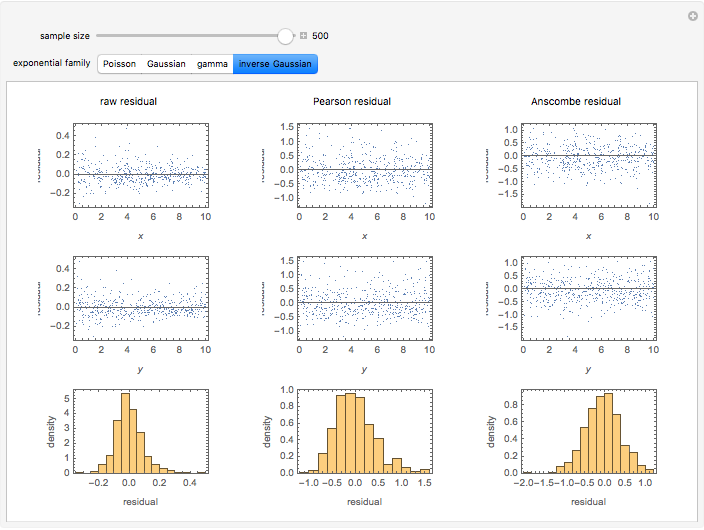
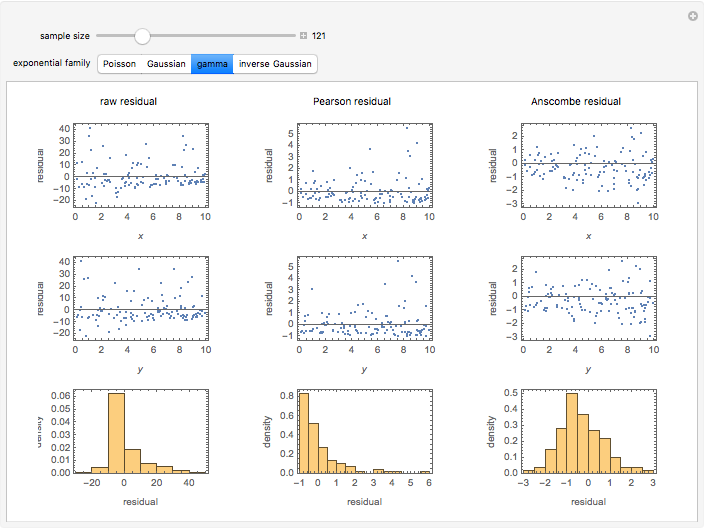
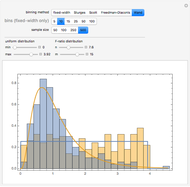
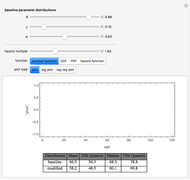
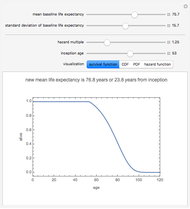
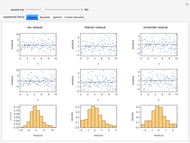
A number of different kinds of residuals are used in the analysis of generalized linear models. Generalized linear models can be characterized by a variance function that is the variance of a distribution as a function of its mean up to a multiplicative constant. A fit or raw residual is the difference between the observed and predicted values. Pearson residuals scale this difference by the square root of the variance function to adjust for the expected variation in the observations. Anscombe residuals provide a transformation toward normality for the assumed variance function.