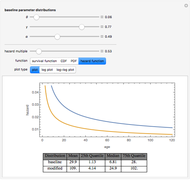
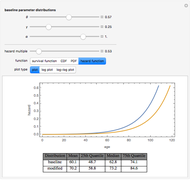
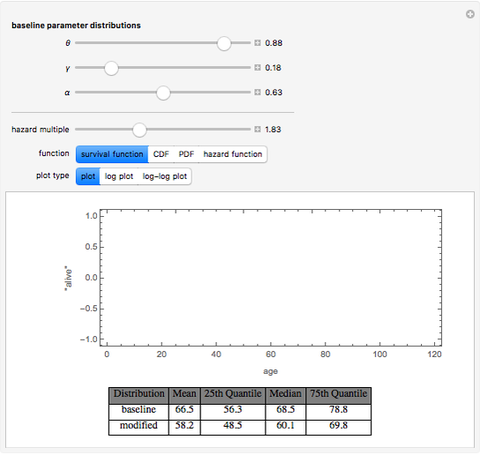
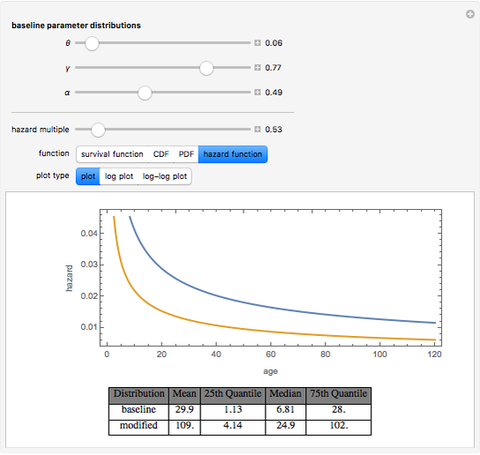
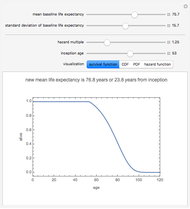
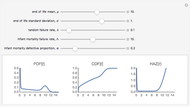
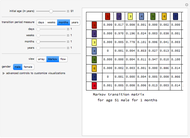
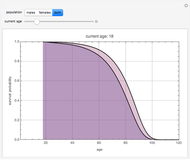
Those involved in examining the duration of phenomena such as physical products or life or legal constructs such as the persistency of an insurance contract often need flexible mathematical models for doing so. One particularly flexible distribution is the so-called expo-power distribution. Unlike less flexible distributions such as the exponential, Weibull, gamma, or Gompertz–Makeham distributions, an expo-power distribution can have hazard functions that are flat, monotonically increasing (e.g. mortality), monotonically decreasing (e.g. insurance contract persistency), U-shaped, or inverted U-shaped. Like the Gompertz–Makeham and Weibull distributions that it nests, the expo-power distribution also has the useful property that a multiple of the hazard function creates a new distribution that is still within the expo-power family. One can thus readily examine questions such as the expected lifetime of an object if one assumes that the hazard confronting that object is a constant percentage of some baseline hazard trajectory. This ability is important because actuaries sometimes use fixed hazard multiples to create mortality tables or lapse tables for subsets of populations for which they have limited data.