Likelihood-Based Goodness of Fit in Two-Way Contingency Tables

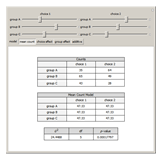
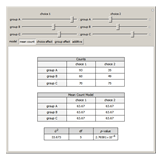
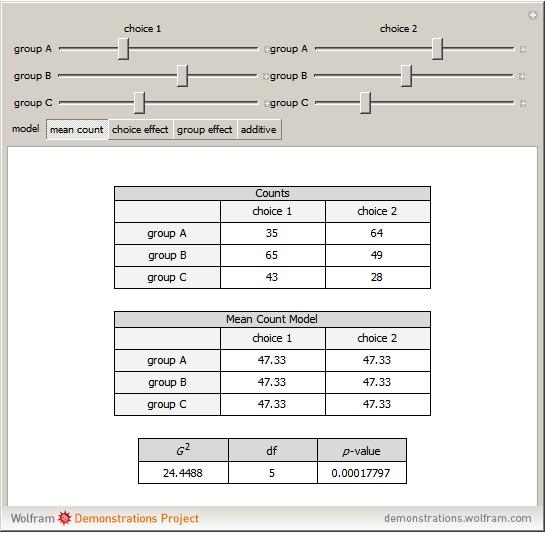
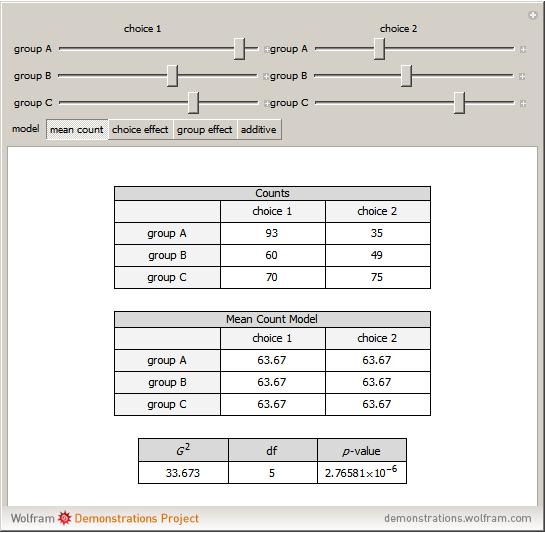
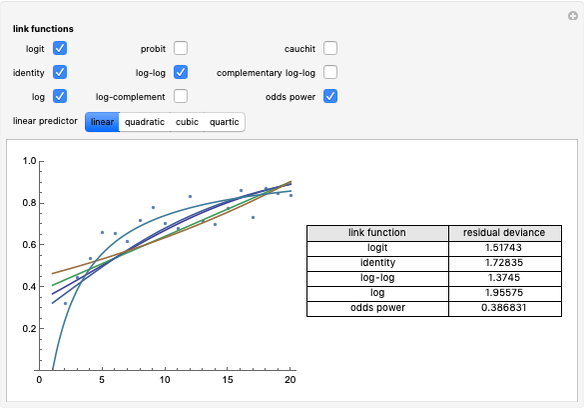
Models of contingency tables are based on the counts by category. In a two-way table, models can depend on either, neither, or both of the categories. The 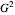likelihood ratio statistic provides a measure of how well a particular model fits the original counts. The null hypothesis is that the chosen model fits the data well. The alternative hypothesis is that the saturated model (the model with predicted counts equal to the actual counts) is needed. A small -value for the statistic indicates the chosen model does not fit the data well. As the counts in the table get large, follows a distribution, and a 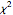approximation can be used to obtain 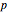a -value provided the predicted counts in the table are not very small.

Use the sliders to adjust the original counts. Select between the four models to get the predicted counts and test statistic for that model of the contingency table.