Maximum Likelihood Estimators for Binary Outcomes

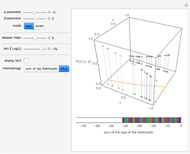
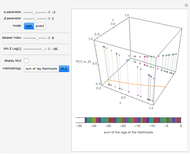
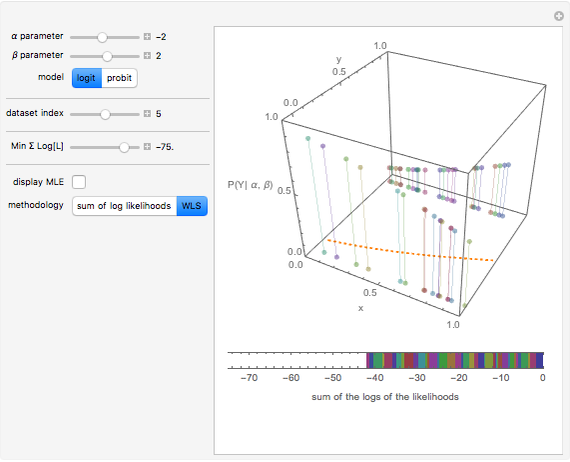
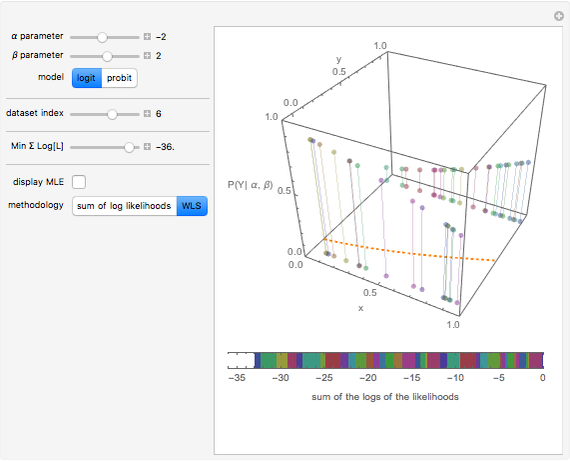
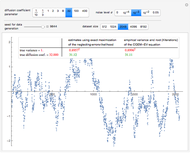
Often regressions involve binary outcome data: the object is to predict some event that will or will not occur based on various data. This Demonstration shows how to derive the maximum likelihood estimates of the coefficients in probit and logit regressions that are typically used to model data with a binary outcome. You can specify a dataset for examination, make guesses as to the and parameters, and choose a logit or probit regression model. The top panel shows the data, the current regression model (orange line) and the probability (likelihood) that each -value would occur for a given -value, given and . The bottom panel shows the sum of the log of each of these likelihoods. 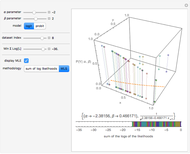Selection of maximum likelihood estimates of and will make this sum as large as possible and the displayed rectangle as small as possible. You can specify the minimum displayed value of the sum of the log likelihoods. If you are curious, you can also request a computation of the correct answer for each dataset, which may be done either directly or using an iterative weighted least squares (WLS) process.