Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Complex Newton Iteration for a Cubic Polynomial

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

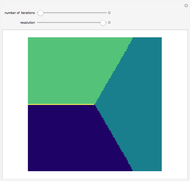
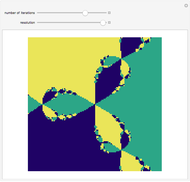
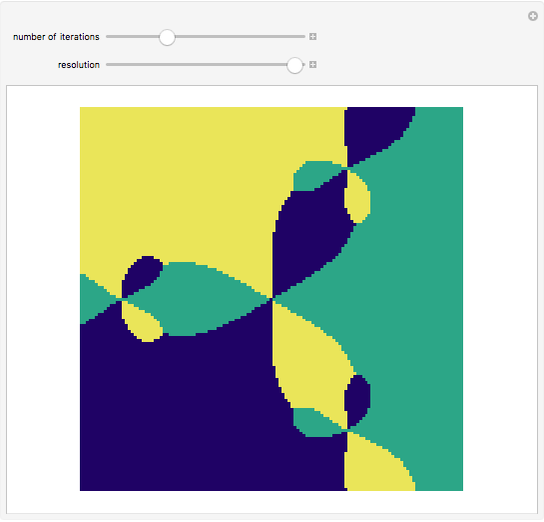
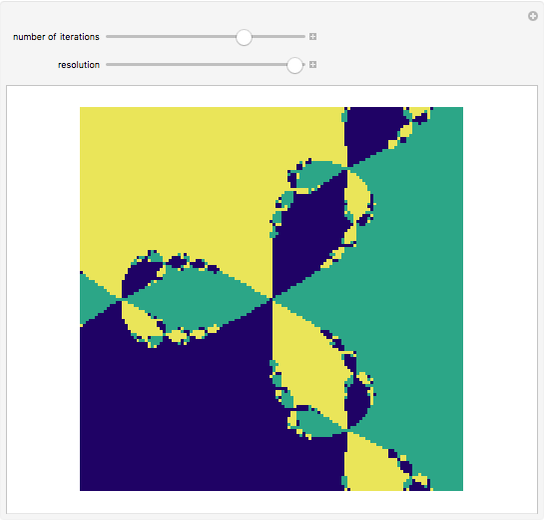
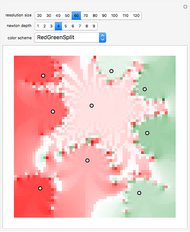
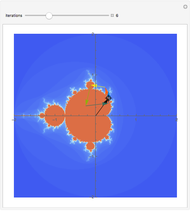
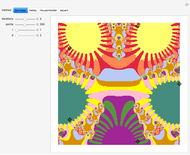
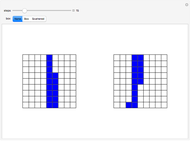
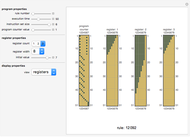
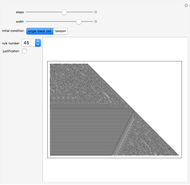
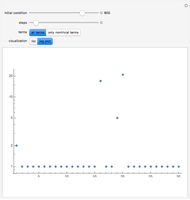
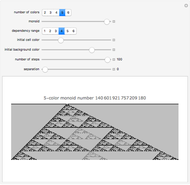
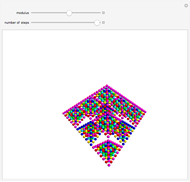
The color at a point indicates in which region of the complex plane it lies after iterations of the map 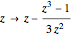. This is Newton's method for finding the complex roots of .

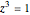Contributed by: Eric Rowland (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: After zero iterations, each point lies in its original region.

Snapshot 2: Nested structure can be seen after three iterations.

Snapshot 3: Intricate patterns develop for higher iterations.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send