Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Simple Unconstrained Optimization Method

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

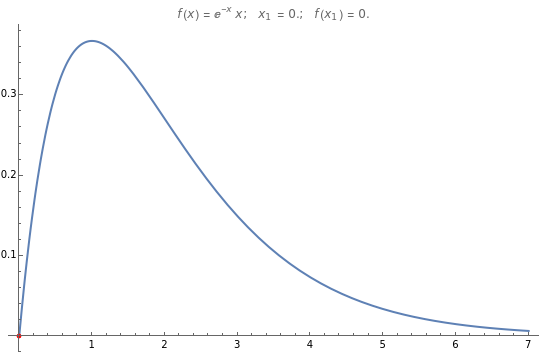
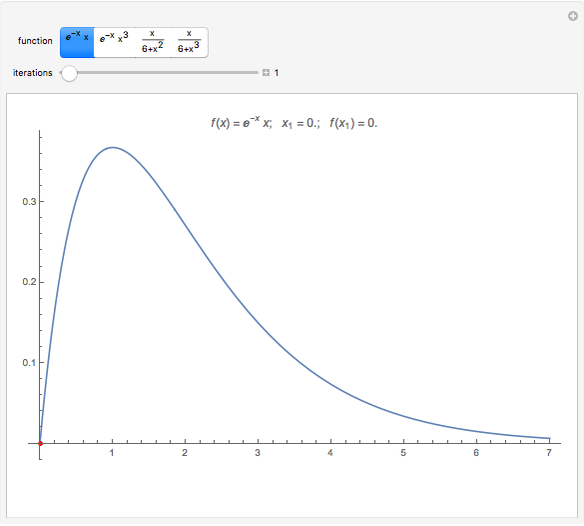
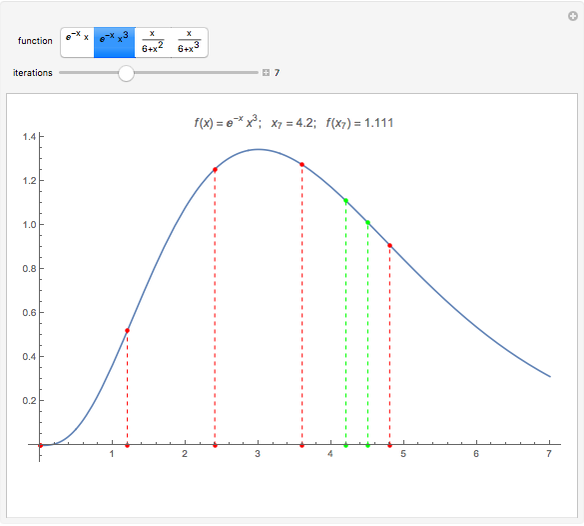
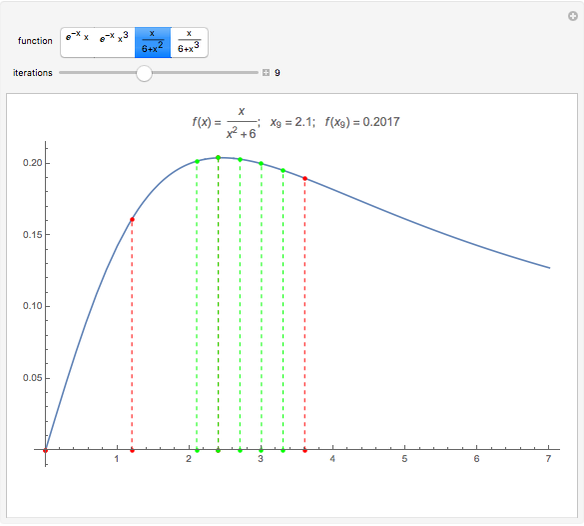
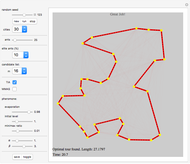
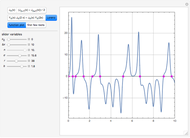
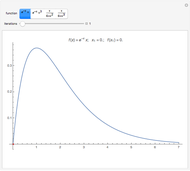
This Demonstration shows the simple one-dimensional unconstrained maximization algorithm for finding the (local) maximum of the function near the starting value 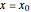. It is a nongradient method and it requires only the starting value 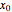and the initial step value .

Contributed by: Marko Petkovic (April 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

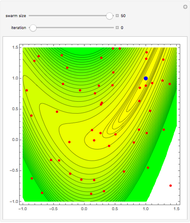
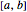Assume that the function has a single local maximum on the interval . For the given real numbers 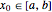and 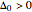, construct the sequences and 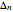in the following way:

.

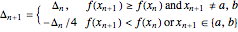It can be proved that the sequence converges to . The method is simple and easy to implement. It does not require the differentiability of the function nor any additional condition on 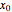and . This method is also known as simplex method I and has a linear convergence.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send