Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

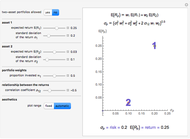
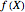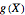Sampling Distribution of the Sample Mean

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

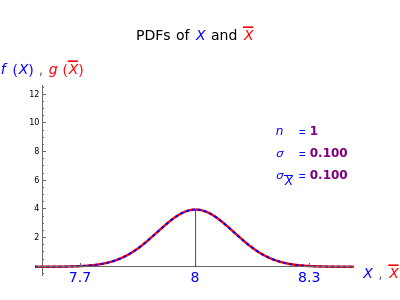
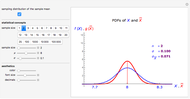
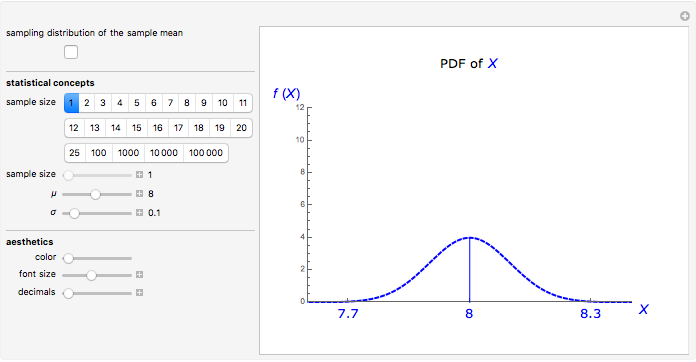
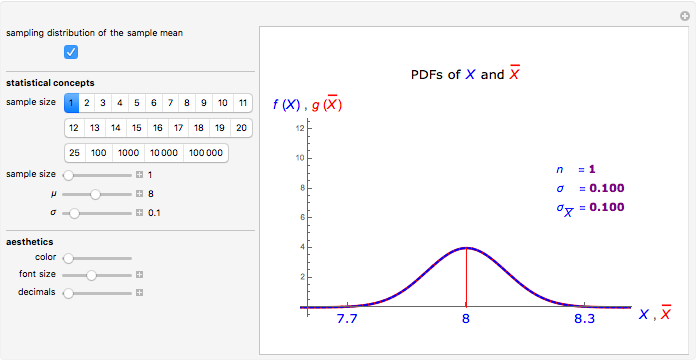
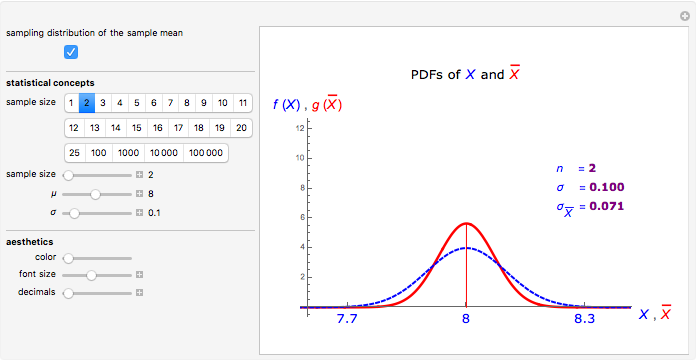
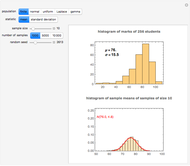
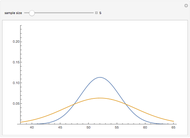
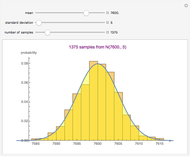
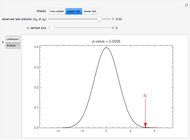
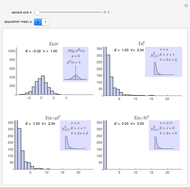
The sample mean is a specific number for a specific sample. The sample mean is a random variable that varies from one random sample to another. Provided the sample size is sufficiently large, the sampling distribution of the sample mean is approximately normal (regardless of the parent population distribution), with mean equal to the mean of the underlying parent population and variance equal to the variance of the underlying parent population divided by the sample size. 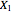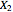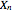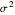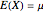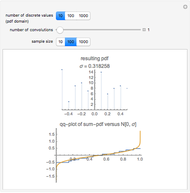More formally, if , ,..., are a random sample from an infinite population with mean and variance then and 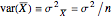; and assuming the moment-generating function of the population exists, the limiting distribution of as approaches infinity is the standard normal distribution (Freund 1992).

[more]

With "sampling distribution of the sample mean" checked, this Demonstration plots probability density functions (PDFs) of a random variable (normal parent population assumed) and its sample mean as the graphs of and respectively.

For given other parameters ( and ), increase the sample size to visualize the effect on the standard error and therefore sampling distribution of the sample mean. As an estimator of an unknown population mean, the sample mean possesses the properties of unbiasedness and consistency, among others. To visualize the consistency property of the sample mean, set the sample size to 100,000 and observe the variance vanish and (given unbiasedness) the distribution of the sample mean collapse onto the parent population mean.

This Demonstration is intended to be an instructional or educational tool for educators and students in introductory statistics and econometrics courses.

[less]

Contributed by: Jim R Larkin (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

J. E. Freund, Mathematical Statistics, 5th ed., Englewood Cliffs, N. J.: Prentice-Hall, 1992.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send