Details

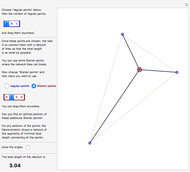
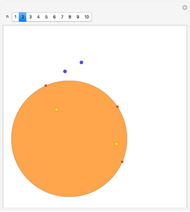
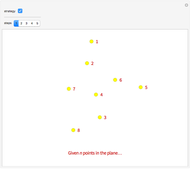
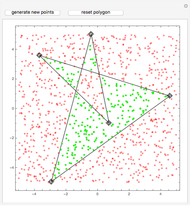
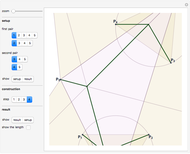
The snapshots illustrate the steps of the construction, which are based on drawing equilateral triangles on two sides of the pentagon formed by the five points.

Snapshot 1: To start, choose the two sides. This is done using the "setup" controls. The order of the endpoints are important because there are two ways of drawing an equilateral triangle on a line segment. Also, because of later steps in the construction, the order of the pairs is also important. A typical case where the construction works is when the points form a convex pentagon and the points for the pairs are chosen counterclockwise.

Snapshot 2: For step 1, draw equilateral triangles on the two chosen sides.

Snapshot 3: The two new vertices of the equilateral triangles and the so-far unused vertex of the pentagon form a triangle. Step 2 finds the Fermat (or Torricelli) point of this triangle (see the Related Links section). This is the first step where the construction can fail: this point must be inside the triangle. If it is not inside, the construction fails.

Snapshot 4: Connect this Fermat point with the vertices of the equilateral triangles and find where these line segments intersect the circumcircles of the equilateral triangles. If these intersection points are not at the right position (on the smaller arc of the circle), the construction cannot continue.

Snapshot 5: To get the Steiner tree, connect the points found with the original points.

Snapshot 6: This shows the Steiner tree without the construction lines. Also, you can turn the display of the total length of the network on and off. Drag the points. It is interesting to see the positions when the construction fails to give a result. In this snapshot, the tree is built using the initial pairs and . There are other pairs for which the construction gives a solution, for example and , or and , and so on. The total lengths of the corresponding networks are not necessarily the same. Try it.

Do you see the similarity of this construction and the one for three and four points (see Related Links)? Can you figure out a way that works for six points?

Can you prove that at the junction points the line segments meet at 120°? This is why the networks found are locally optimal, in the sense that moving any junction point a bit will increase the total length of the network. This only means that the total distance cannot be improved by moving the junction points a bit; in other words the construction gives a locally optimal solution. It does not mean that a completely different construction cannot give a better network. However, it is generally true that the globally optimal network has the property that the angle between any two adjacent line segments is not less the 120° and at any added points exactly three line segments meet at 120°. In some arrangements of the original points this means that one of the local minima found with this construction (with different starting pairs) will give the globally optimal network.