Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Jarvis March to Find the Convex Hull of a Set of Points in 2D

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

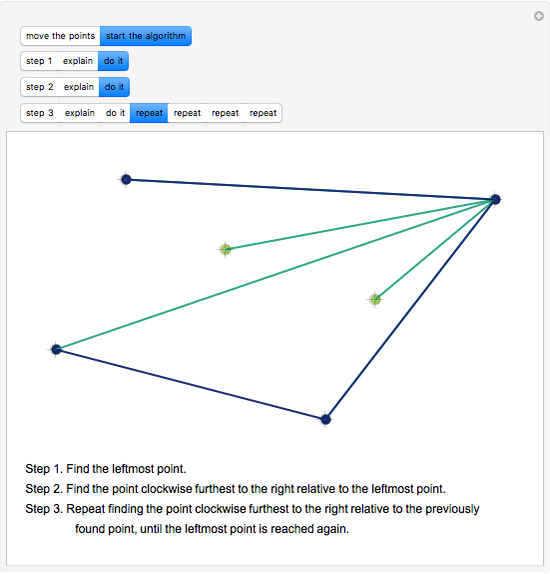
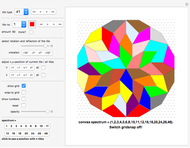
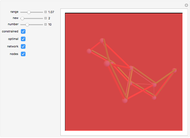
This Demonstration illustrates the steps of the Jarvis march, an algorithm to find the convex hull of a finite set of points in 2D. It is not the fastest possible algorithm in general, but is conceptually simple. It is also called the "gift wrapping algorithm", because it finds the vertices of the convex hull in counterclockwise order (or clockwise order, depending on the implementation).

Contributed by: Ferenc Beleznay (October 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

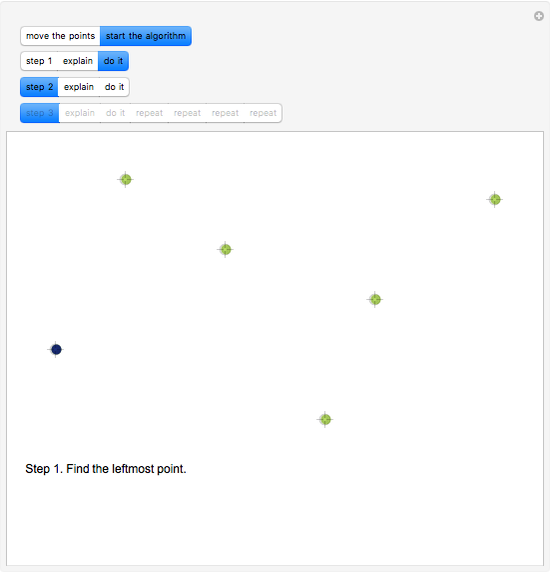
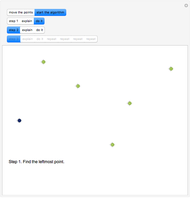
Snaphot 1: the first step of the algorithm is to find an extreme point (any vertex of the convex hull)

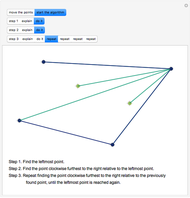
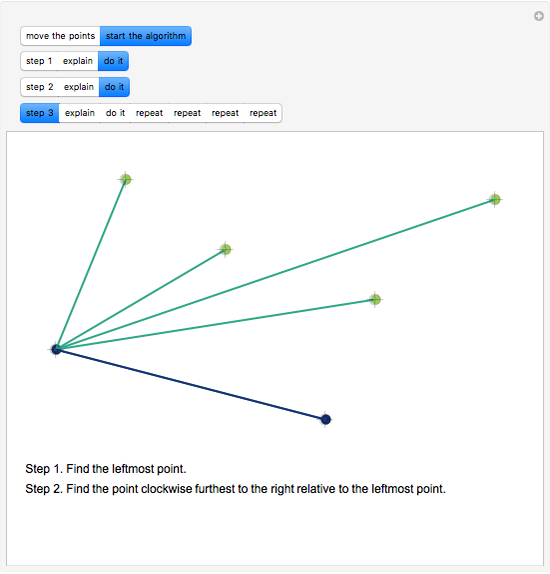
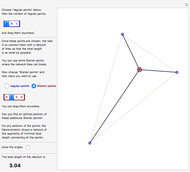
Snaphot 2: we then find the next vertex of the convex hull in a counterclockwise order by examining the directions of the halflines from the first point toward all the other points

Snaphot 3: repeating the previous step, we find the vertices of the convex hull one by one

When we reach the first point, the convex hull is found.

The algorithm used to find the convex hull in this Demonstration is the implementation of the one from Tom Switzer's website: "2D Convex Hulls: Jarvis March".

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send