Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

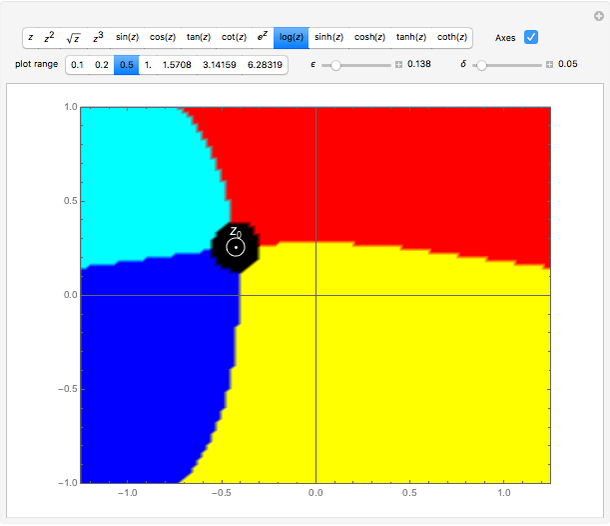
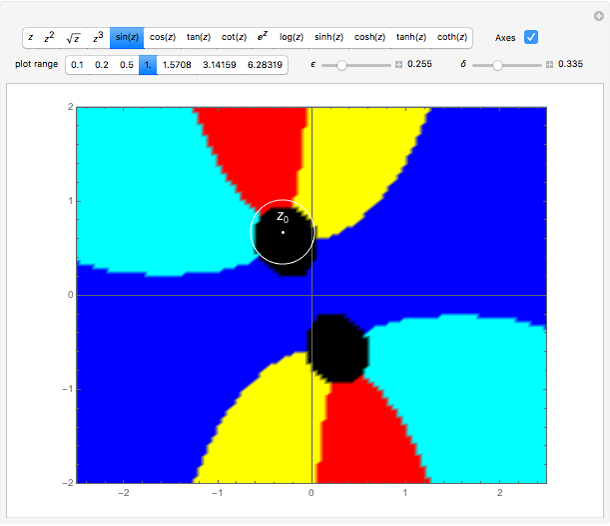
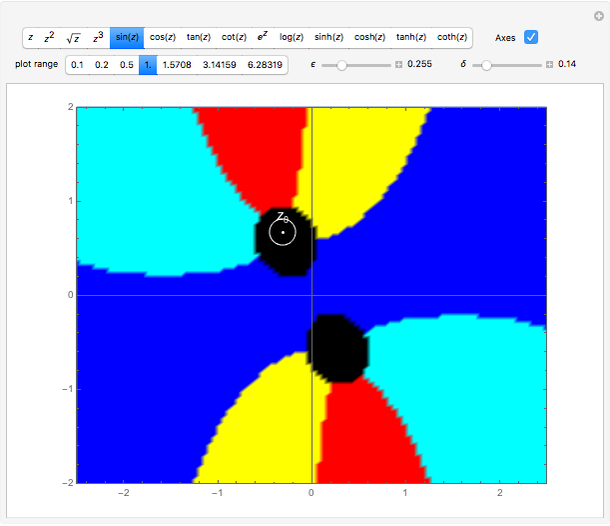
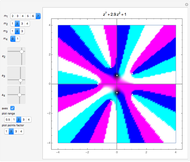
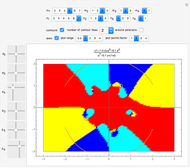
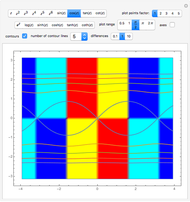
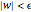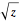Continuity of a Complex Function

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

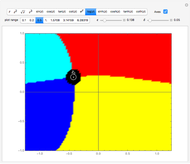
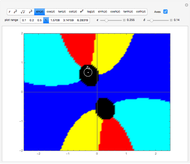
Let be a complex function where 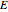and 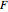are open subsets in . The function is continuous at the point if for every there is a such that for all points that satisfy the inequality , the inequality holds.

[more]

We assign a color to each point of the complex plane as a function of , namely the RGB color of four arguments , , , and (red, green, blue, and opacity). If (with chosen by the slider), we use black. Otherwise, if , ; if , ; if , .

A black patch around the point means that the function has . After that, we find a such that the circle is inside the patch. Note the branch cut for along the negative real axis.

[less]

Contributed by: Izidor Hafner (February 2016)
Open content licensed under CC BY-NC-SA

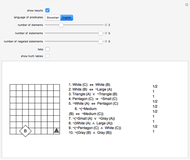
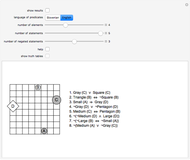
Snapshots

Details

References

[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015 pp. 35–36.

[2] A. G. Sveshnikov and A. N. Tikhonov, The Theory of Functions of a Complex Variable, Moscow: Mir Publishers, 1971 pp. 24–25.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send