Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Decomposition of Some Polygons to Iso-Penta Triangles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

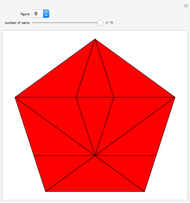
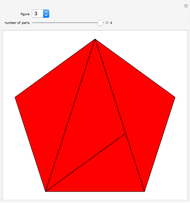
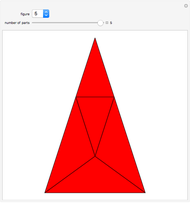
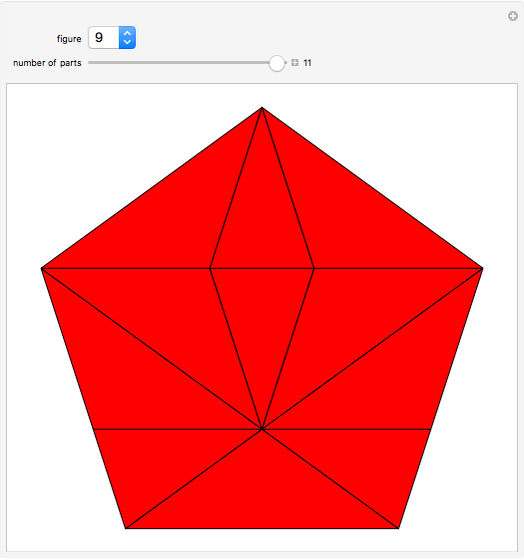
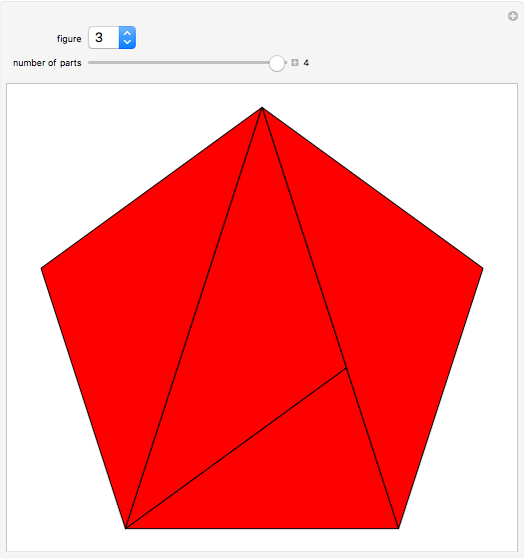
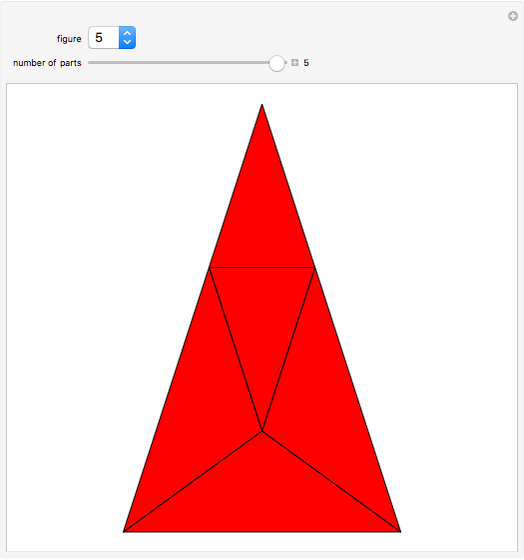
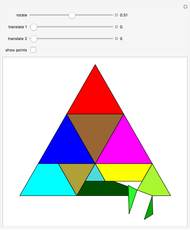
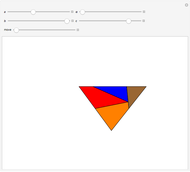
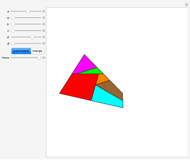
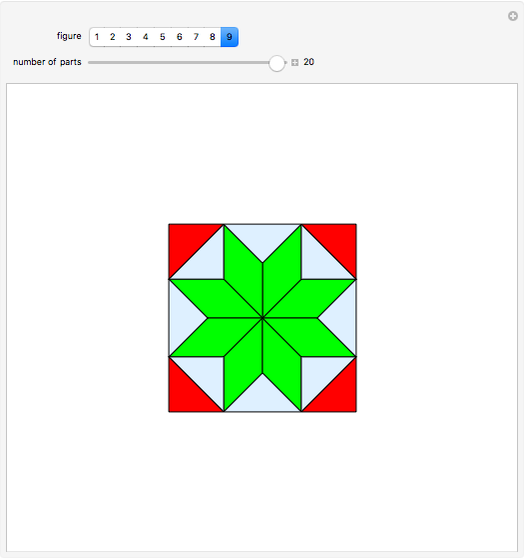
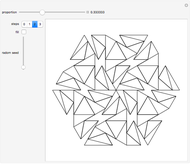
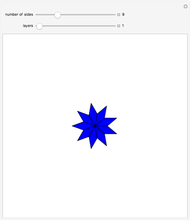
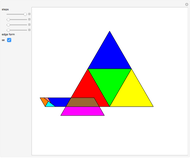
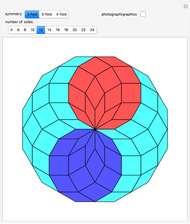
Many figures, such as the pentagon, pentagram, and decagon, can be dissected into isosceles triangles where all three angles are multiples of 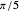. Such triangles are called iso-penta triangles.

Contributed by: Izidor Hafner (September 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] G. N. Frederickson, Dissections: Plane & Fancy, New York: Cambridge University Press, 1997 p. 212. www.cs.purdue.edu/homes/gnf/book.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send