Dissection of Three Bilunabirotundas and a Dodecahedron into Rhombic Solids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
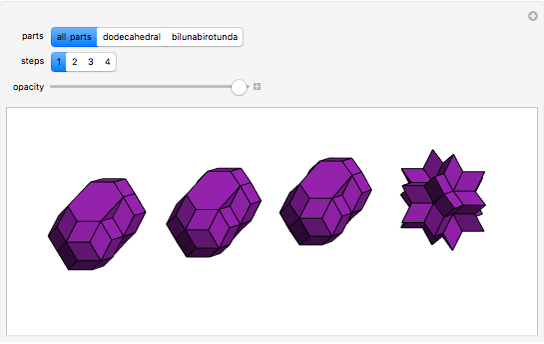
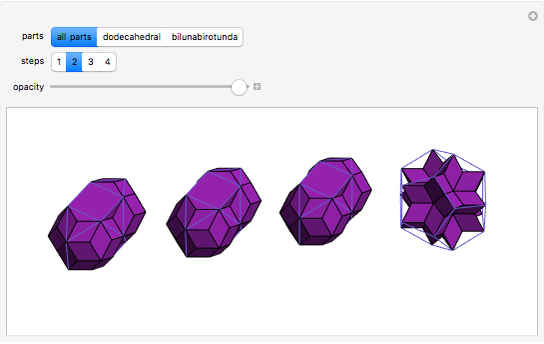
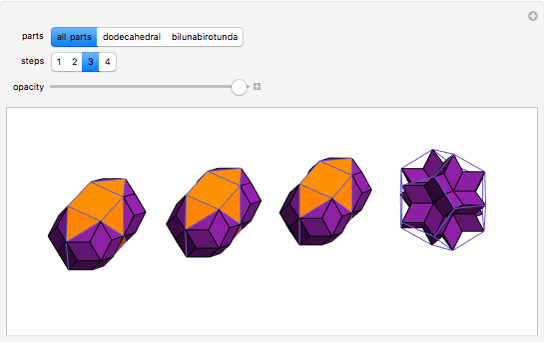
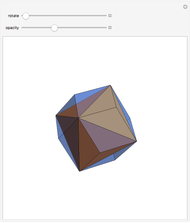
This Demonstration shows a dissection of three bilunabirotundas and a dodecahedron into rhombic solids.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
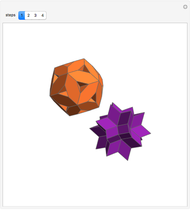
The decomposition of a combination of solids to a combination of rhombohedra means that the former can be decomposed to the cube as well [1]. In [2], visual evidence is given that three bilunabirotundas (Johnson solid 91) and the dodecahedron can be decomposed into three rhombic solids and a rhombic hexecontahedron.
A bilunabirotunda inscribed in the "rhombic" solid has a deficit of four pentagonal cups, while triangular pyramids annihilate one another. On the other hand, the dodecahedron has a surplus of 12 pentagonal cups that annihilate the deficit of 12 cups of the bilunabirotundas. That such a dissection is possible also follows from the Demonstration referenced in Related Links.
[1] V. G. Boltyanskii, Tretja Problema Hilberta, Moscow: Nauka, 1977. Translated by R. A. Silverman as Hilbert's Third Problem (New York: John Wiley & Sons, Inc., 1978). [2] I. Hafner, "Decomposition of Three Bilunabirotundas and Dodecahedron to Rhombic Solids," Visual Mathematics, 9(2), 2007 article 6.