Dissection of Three Rhombic Solids into an Icosahedron, a Dodecahedron, and an Icosidodecahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
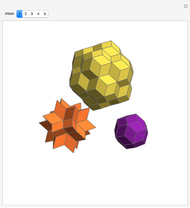
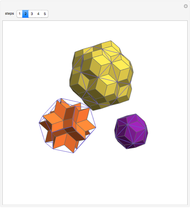
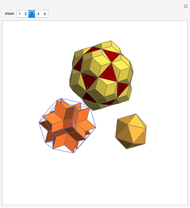
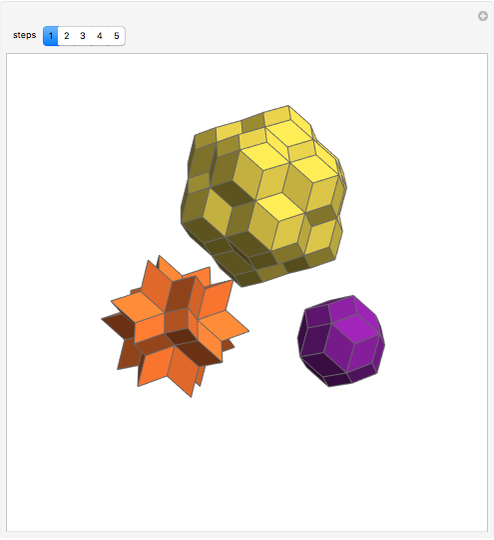
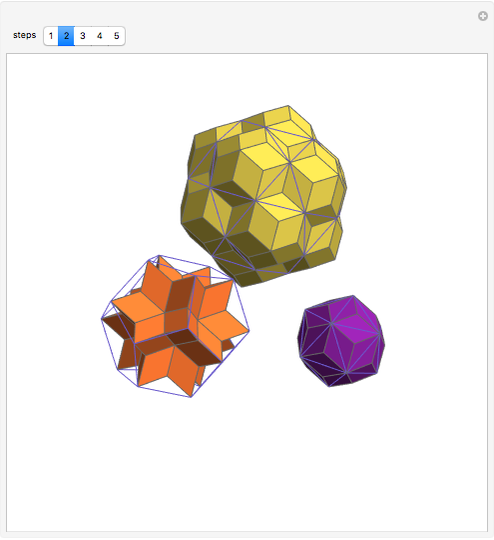
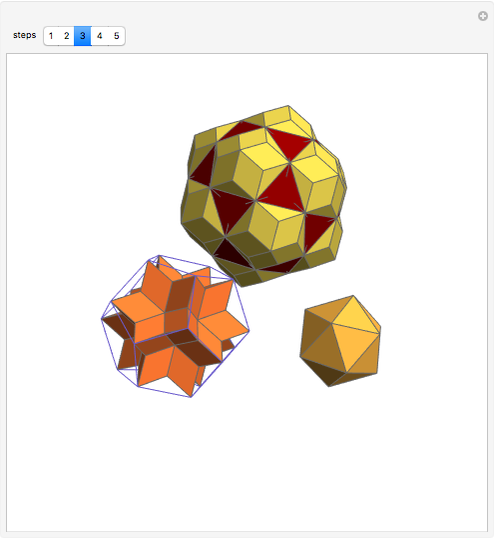
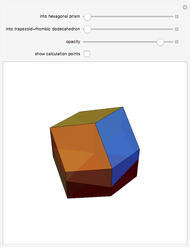
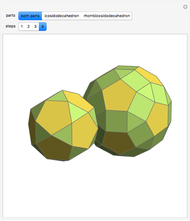
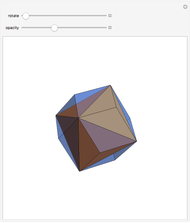
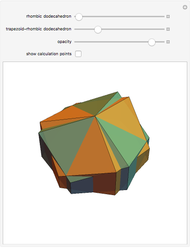
This Demonstration gives a dissection of the union of a rhombic triacontahedron, a hexecontahedron, and a 120-hedron into the union of an icosahedron, a dodecahedron, and an icosidodecahedron.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It was proved [1] that the combination of the icosahedron, the dodecahedron, and the icosidodecahedron has Dehn invariant 0, so by Sydler's theorem it is possible to dissect the combination to form a cube. In a related Demonstration (see Related Links), an example is given of a dissection of this combination to rhombic solids. In this Demonstration the connection of combinations is done using the larger diagonal of the golden rhombus.
[1] J. H. Conway, C. Radin, and L. Sadun, "On Angles Whose Squared Trigonometric Functions Are Rational," Discrete & Computational Geometry, 22(3), 1999 pp. 321–332.