Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Distance of a Point to a Segment

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

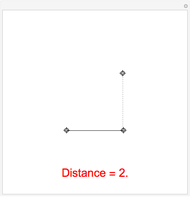
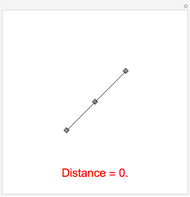
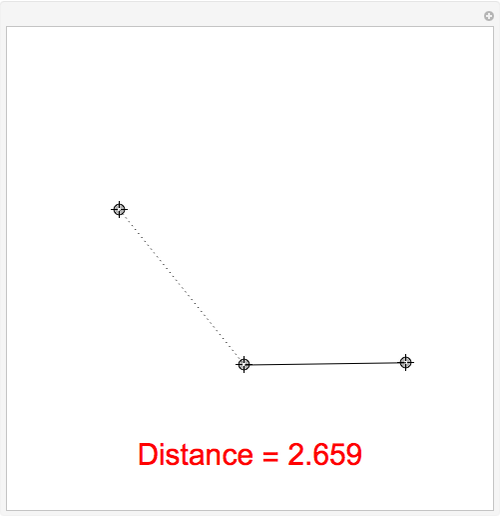
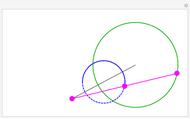
The distance of a point to a segment is the length of the shortest line joining the point to a point on the segment. This Demonstration depicts this shortest line as dotted. The measurements are normalized so that the point starts at a distance of 1 to the segment.

Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

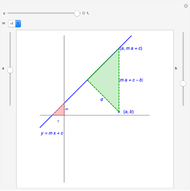
To compute the distance from point p to segment ab (all as complex numbers) compute first z=(p-a)/(b-a). If 0 ≤ Re[z] ≤ 1 then the distance is equal to Abs[Im[z](b-a)]. If not, it is equal to the smallest of the distances from p to a or to b.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send