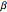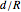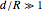Eigenvalues and Eigenfunctions for Angular Double-Well Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
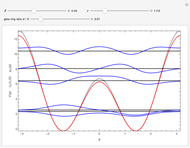
This Demonstration presents the quantum-mechanical problem of a particle confined to a ring under the influence of a symmetric double quantum well (DQW) potential along the angular coordinate. The Schrödinger equation is solved for the allowed energy levels and the corresponding wavefunctions. One realization of this system might be a single-electron semiconductor quantum ring placed between two lateral gates, which we model as parallel negatively charged wires equidistant from the ring center and lying in the plane of the ring.
[more]
Contributed by: Thomas P. Collier (June 2019)
Open content licensed under CC BY-NC-SA
Details
We study the lowest single-electron energies and wavefunctions obeying the Schrödinger equation. The dimensionless external potential felt by an electron of charge 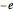 and effective mass
and effective mass  , confined between two in-plane gates is given by
, confined between two in-plane gates is given by
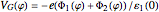 ,
,
where  is the energy scale of the interlevel separation in the ring of radius
is the energy scale of the interlevel separation in the ring of radius  , and
, and 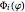 is the electrostatic potential along the ring due to an individual negatively charged gate. We model the gates as charged wires, as in [1]. Thus the individual wire electrostatic potential is given by
is the electrostatic potential along the ring due to an individual negatively charged gate. We model the gates as charged wires, as in [1]. Thus the individual wire electrostatic potential is given by
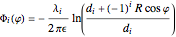 .
.
Here 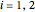 labels the wires,
labels the wires, 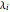 is the linear charge density on a wire, and
is the linear charge density on a wire, and 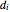 is its corresponding distance from the center of the ring. Zero potential is defined to be along the axis perpendicular to the reflection axis
is its corresponding distance from the center of the ring. Zero potential is defined to be along the axis perpendicular to the reflection axis 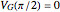 . For simplicity, equidistant gates
. For simplicity, equidistant gates 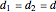 are assumed. Making the approximation
are assumed. Making the approximation 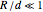 , we can expand
, we can expand 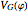 up to second-order terms, which leads to the Hamiltonian
up to second-order terms, which leads to the Hamiltonian
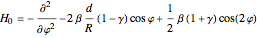 ,
,
where
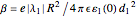
characterizes the global potential strength in terms of the contribution from gate  . The relative contribution from gate
. The relative contribution from gate 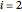 is given by
is given by
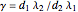 .
.
We have accordingly shifted all calculated values by the arbitrary constant resulting from the expansion. Note that the approximated potential here is a corrected form of the potential used in [1–3] (which has a (harmless) error in the parameter in front of 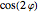 ). Solutions must be
). Solutions must be 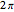 -periodic due to the ring periodic boundary conditions and are found as a sum of free particles on a ring basis function
-periodic due to the ring periodic boundary conditions and are found as a sum of free particles on a ring basis function
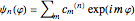 .
.
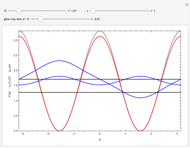
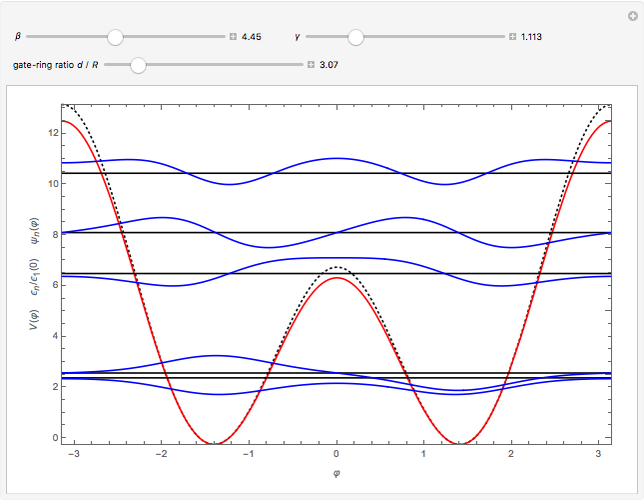
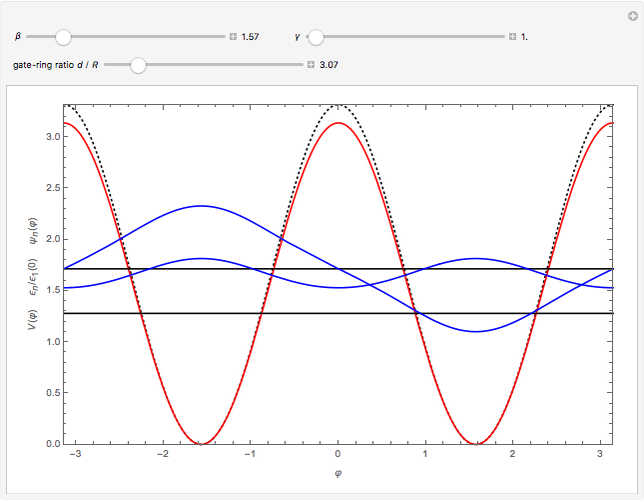
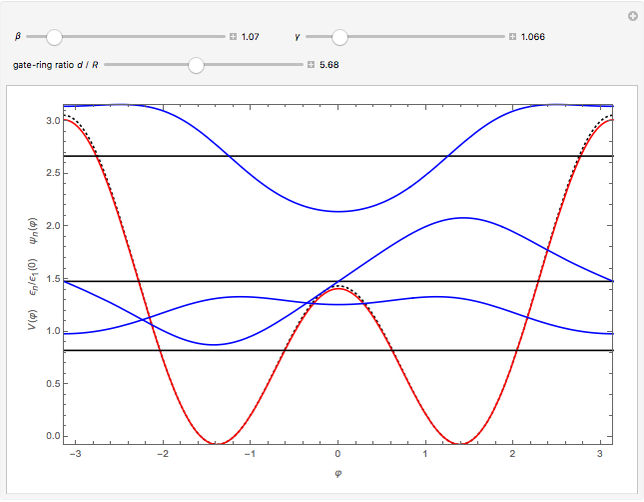
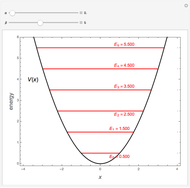
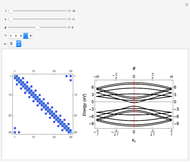
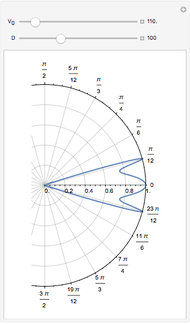
The Demonstration plots the energy levels and wavefunctions for the Hamiltonian 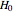 , as well as the approximate trigonometric potential for
, as well as the approximate trigonometric potential for  (red) and the full potential
(red) and the full potential 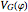 (dotted black), as functions of
(dotted black), as functions of 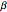 ,
,  and the ratio
and the ratio 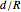 .
.
Snapshot 1: results for equivalent gate contributions 
Snapshot 2: results for non-equivalent gate contributions 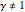 and small global potential strength
and small global potential strength
Snapshot 3: results for deep global potential strength and non-equivalent gate contributions
References
[1] T. P. Collier, V. A. Saroka and M. E. Portnoi, "Tuning Terahertz Transitions in a Double-Gated Quantum Ring," Physical Review B, 96, 2017, 235430. doi:10.1103/PhysRevB.96.235430.
[2] T. P. Collier, V. A. Saroka and M. E. Portnoi, "Tuning THz Transitions in a Quantum Ring with Two Gates," Physics, Chemistry and Applications of Nanostructures (V. E. Borisenko, S. V. Gaponenko, V. S. Gurin and C. H. Kam, eds.), Singapore: World Scientific, 2017 pp. 172–175. doi:10.1142/9789813224537_0040.
[3] T. P. Collier, A. M. Alexeev, C. A. Downing, O. V. Kibis and M. E. Portnoi, "Terahertz Optoelectronics of Quantum Rings and Nanohelices," Semiconductors, 52(14), 2018 pp. 1813–1816. doi:10.1134/S1063782618140075.
Snapshots
Permanent Citation