Eigenfunctions of a 1D Quantum System with Adjustable Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
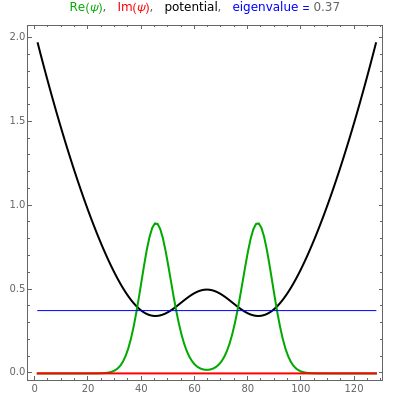
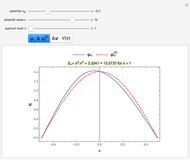
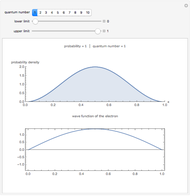
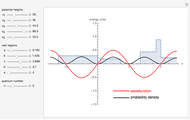
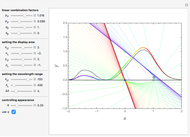
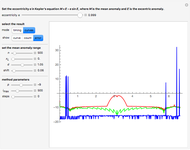
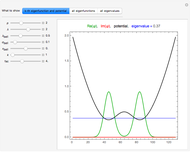
This Demonstration shows the stationary states (eigenvalues and eigenfunctions of the Hamiltonian) for a quantum particle in one dimension under the influence of an adjustable potential. The potential is a sum of two components: (1) a power potential, symmetric for even exponent (such as the default value 2 for the harmonic oscillator) and antisymmetric for odd exponent (e.g., 1 for the inclined plane) and (2) a Gaussian potential barrier. If the barrier (you can select the height, width, and center position) is set appropriately, it turns the harmonic oscillator potential into a double-well potential, an extensively studied quantum-mechanical model system. For the stationary states, you can choose between three graphical representation modes. The most detailed information is obtained in the first of these modes, showing the potential as well as the real and imaginary parts of the eigenfunctions. You can select the stationary state to be displayed. The index  shows how increasingly higher excited states change the geometrical features of the wavefunctions. You can also observe how the energy eigenvalue increases correspondingly.
shows how increasingly higher excited states change the geometrical features of the wavefunctions. You can also observe how the energy eigenvalue increases correspondingly.
Contributed by: Ulrich Mutze (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration is based on the representation of the Hamiltonian operator as a numerical square matrix and on the Mathematica function EigenSystem to determine the eigenvalues and eigenfunctions of this matrix numerically. Unlike analytical methods, the form of the potential is not restricted. The dynamical evolution of initially bell-shaped states in exactly the potentials of the present Demonstration is studied in the Demonstration "Quantum Dynamics in 1D" by the present author.
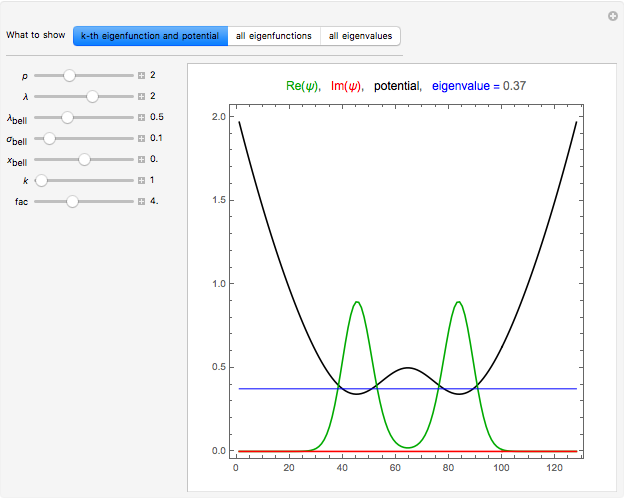
Snapshot 1: symmetric ground state in a symmetrical double-well potential
Snapshot 2: antisymmetric ground state in a symmetrical double-well potential; the lowest energy value is thus degenerate
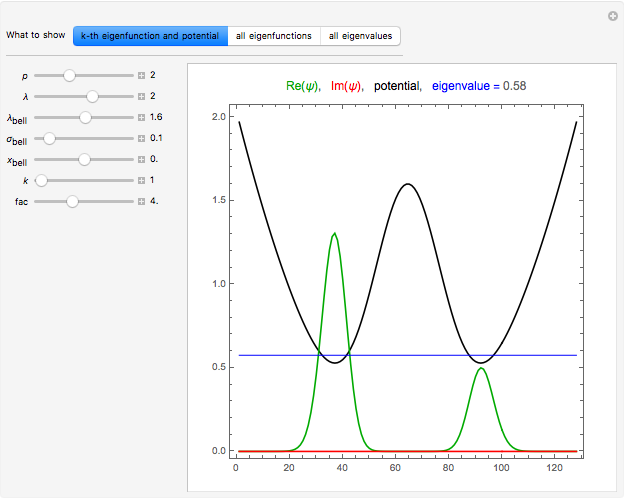
Snapshot 3: ground state in an asymmetrical double-well potential; the lowest energy value is not degenerate
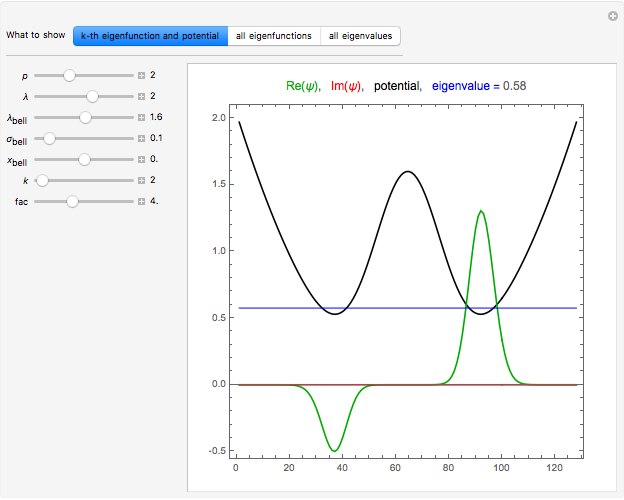
Snapshot 4: first excited state in an asymmetrical double-well potential
Snapshot 5: a highly excited state in a strongly asymmetrical double-well potential
Snapshot 6: all stationary states of the strongly asymmetrical double-well potential
Snapshot 7: all energy values of the particle in the strongly asymmetrical double well potential
Permanent Citation
"Eigenfunctions of a 1D Quantum System with Adjustable Potential"
http://demonstrations.wolfram.com/EigenfunctionsOfA1DQuantumSystemWithAdjustablePotential/
Wolfram Demonstrations Project
Published: January 15 2015