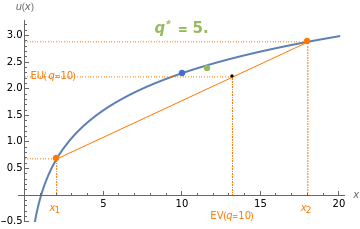
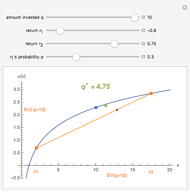
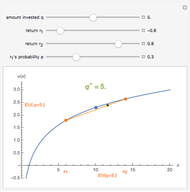
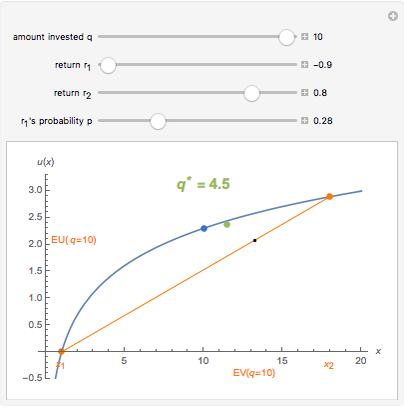
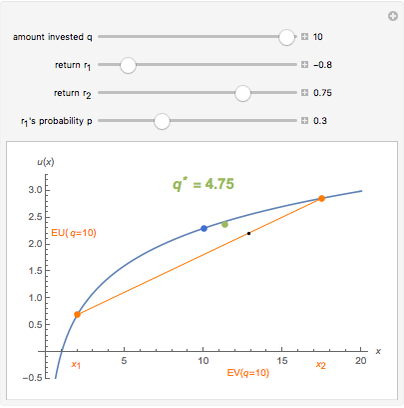
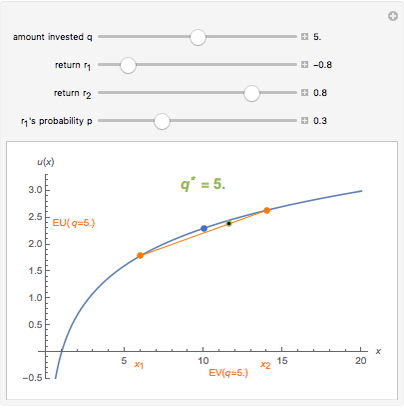
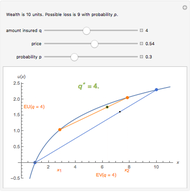
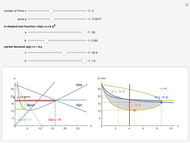
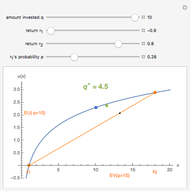
An investor begins with 10 units of wealth that can be invested in a risky asset, or maintained as cash with no return. Assume the risky asset yields a rate of return of or with probabilities and , respectively, and let be the number of units of wealth that the investor decides to invest in the asset. The value of the investor's portfolio at the end of the period will be . 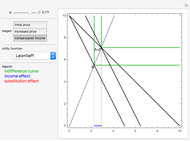Let the two possible end-of-period values of the portfolio be and , shown above along the horizontal axis. The Bernoulli logarithmic utility function of wealth (constant relative risk aversion, CRRA) is plotted in blue. The orange line is a plot of the expected value and the corresponding expected utility of the portfolio for different values of . The optimal portfolio is the one for which the expected utility is a maximum, as shown by the green dot.