Constant Risk Aversion Utility Functions

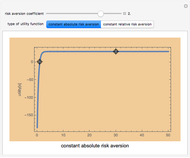
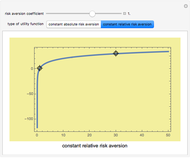
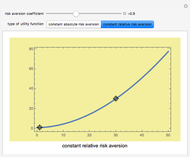
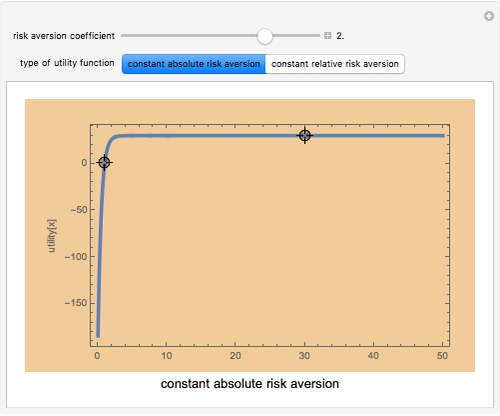
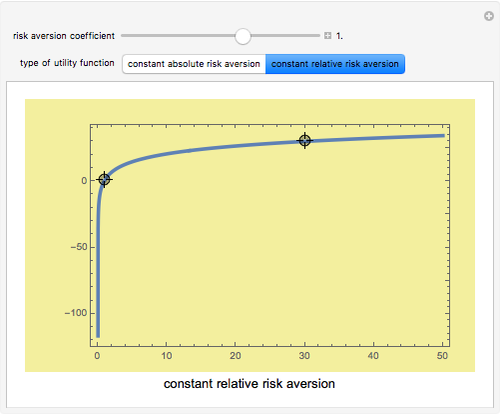
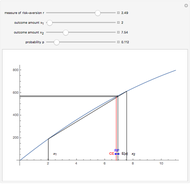
Utility functions are said to exhibit constant risk aversion under the Arrow–Pratt measure if they satisfy a second-order differential equation. You can set a risk aversion coefficient—the higher it is, the more risk averse—as well as the values at two points along the curve; this Demonstration plots the resulting utility function. You can choose between constant absolute risk aversion and constant relative risk aversion. The class of utility functions shown in this Demonstration are frequently used in economic analyses of risk, including finance and insurance.