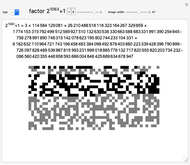
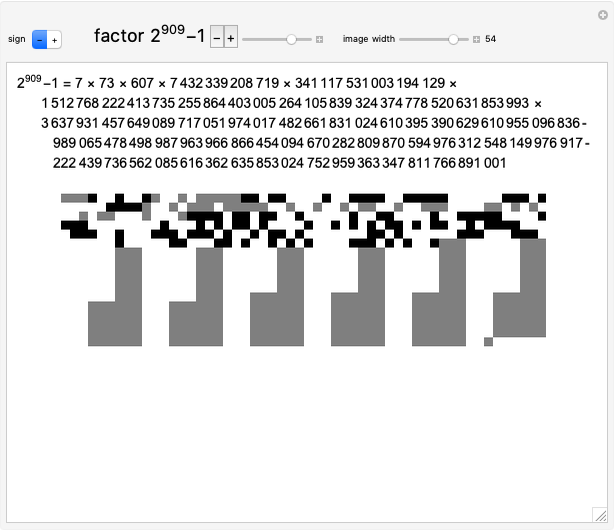
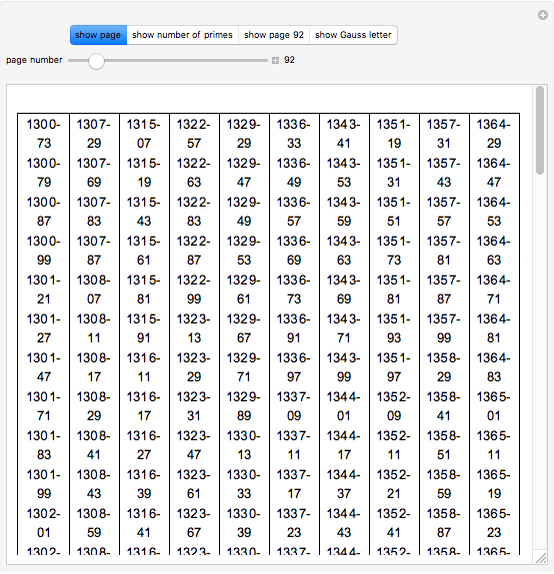
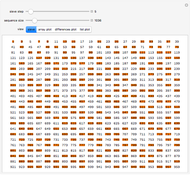
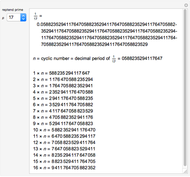
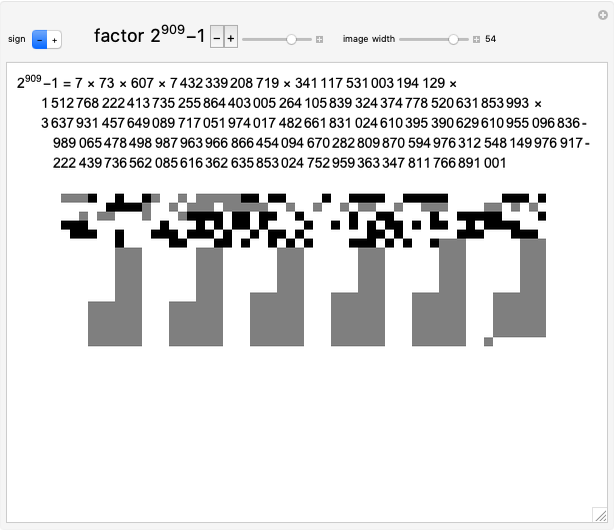
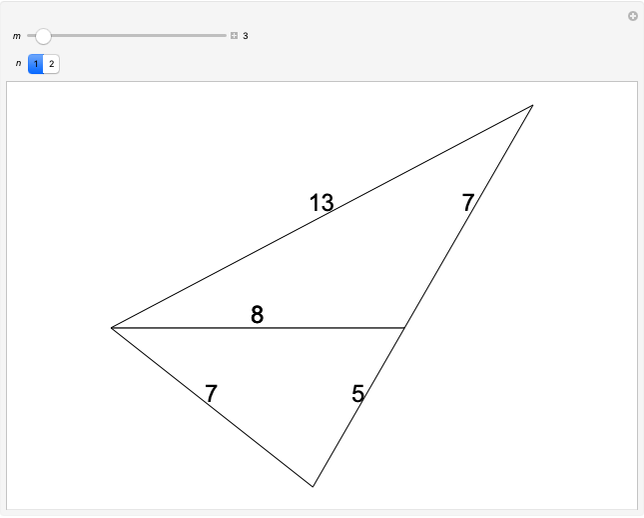
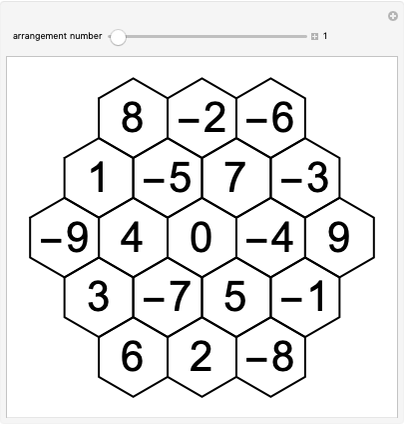
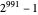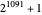Factorizing Mersenne Numbers
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
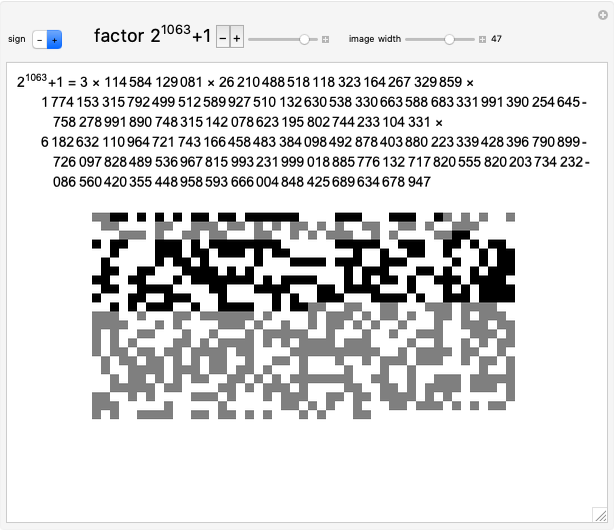
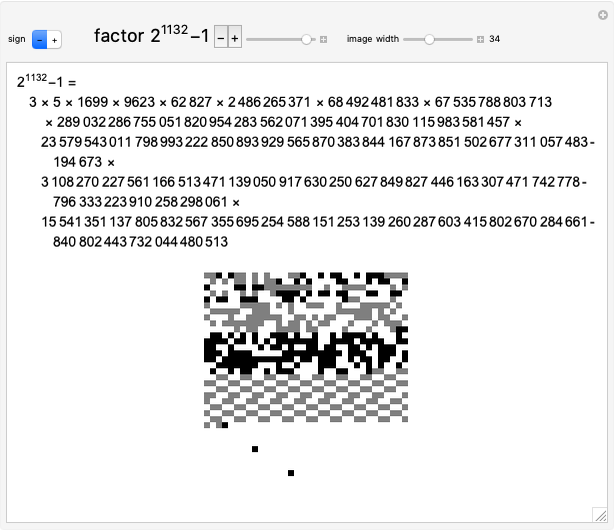
A number of the form 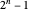 is a Mersenne number, named after Marin Mersenne (1588–1648). If the resulting number is prime, then it is called a Mersenne prime, with
is a Mersenne number, named after Marin Mersenne (1588–1648). If the resulting number is prime, then it is called a Mersenne prime, with 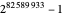 (or M82589933) currently the largest known prime.
(or M82589933) currently the largest known prime.
Contributed by: Ed Pegg Jr (July 2015)
Open content licensed under CC BY-NC-SA
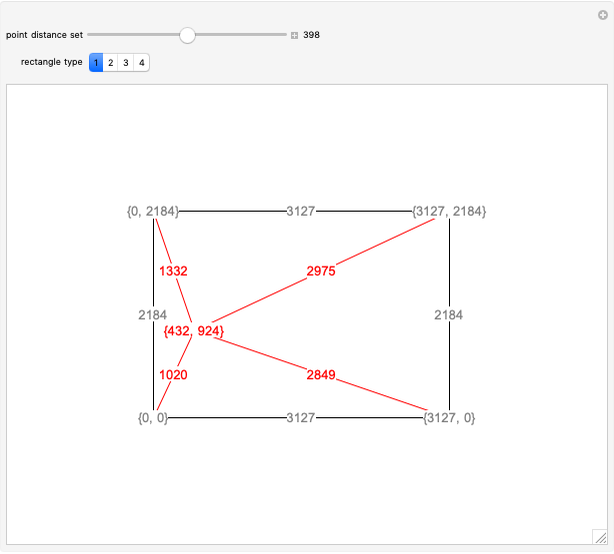
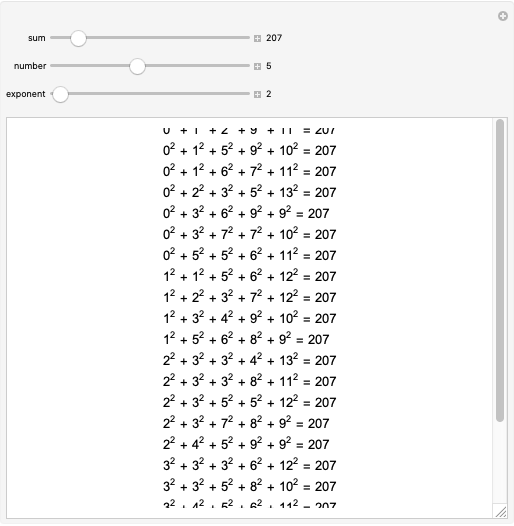
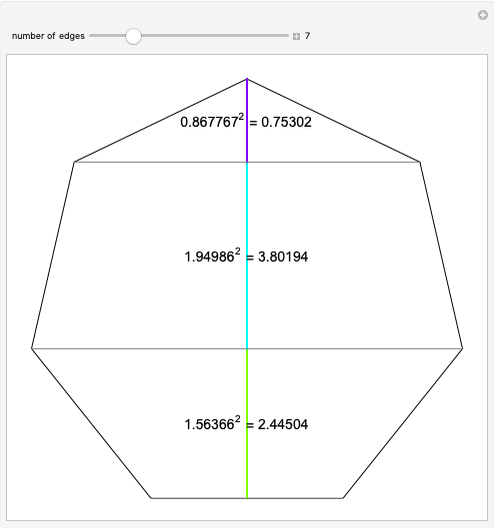
Snapshots
Details
References
[1] S. Wagstaff. "The Cunningham Project". (Jul 12, 2015) homes.cerias.purdue.edu/~ssw/cun/index.html.
Permanent Citation