Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Relatively Prime Numbers and Zeta(2)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

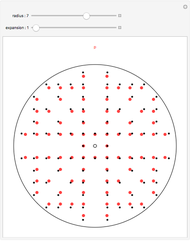
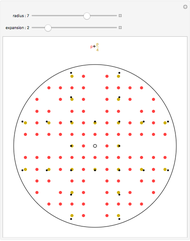
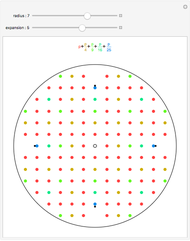
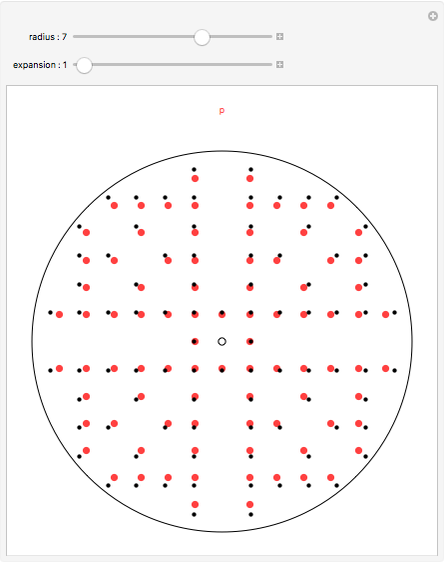
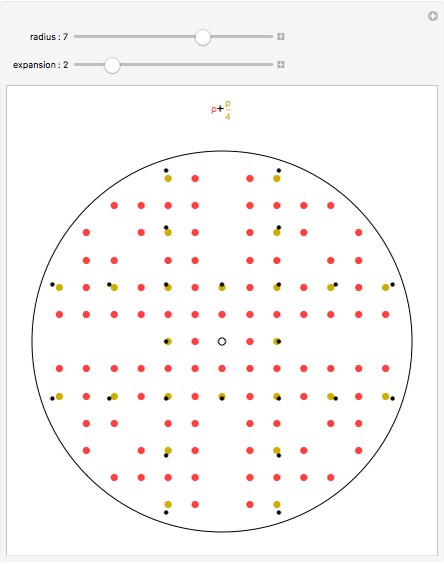
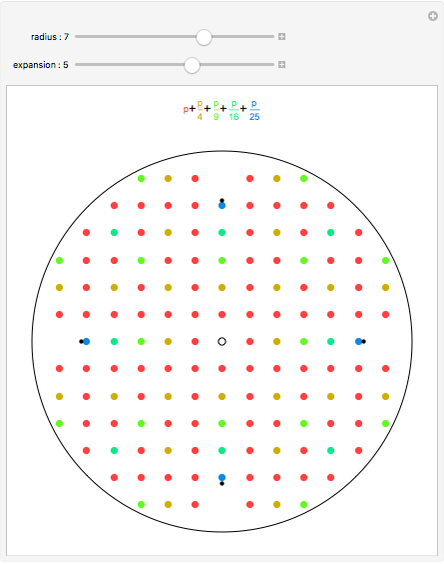
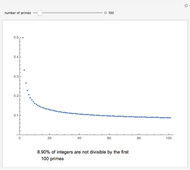
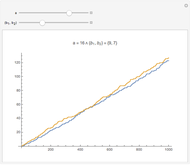
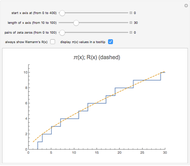
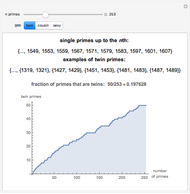
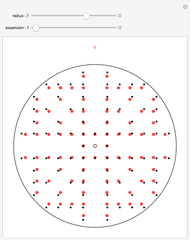
Two integers are relatively prime if they share no common positive factors (divisors) except 1. In the graphic the points have integer and coordinates. If an integer pair consists of relatively prime numbers, no other such point lies on the line between the origin and this point.

[more]

With no expansion, the distribution of relatively prime pairs is shown and their density (or probability) is expressed as . When this distribution is expanded by , their density is reduced by the square of . Because there is no intersection between the expansion sets, the individual densities can be summed to obtain the overall density, which is 1. Therefore is obtained as , which is equal to .

[less]

Contributed by: Okay Arik (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send