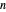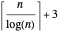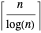Mondrian Art Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
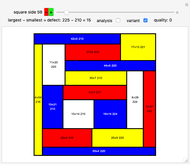
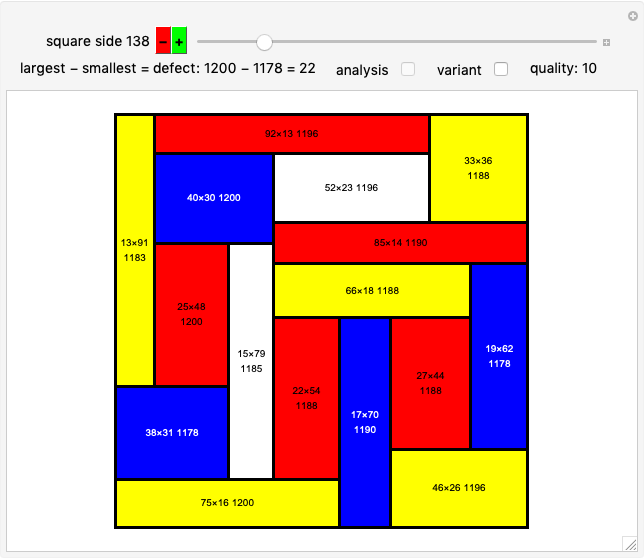
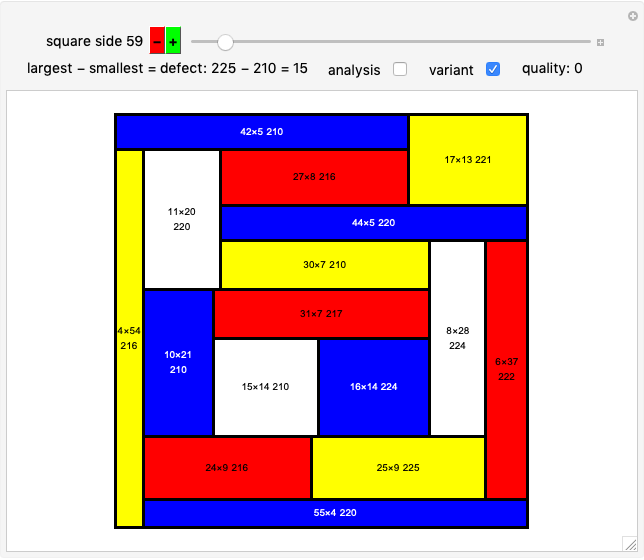
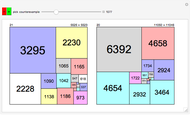
Divide a square into non-congruent rectangles. If all the sides are integers, what is the smallest possible difference in area between the largest and smallest rectangles? This is known as the Mondrian art problem. This Demonstration shows optimal solutions up to size 65 and best known solutions up to 900.
[more]
Contributed by: Ed Pegg Jr (November 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The defect 8 solution for the 18×18 square was found by Bruce Norskog. Solutions for cases 14×14, 16×16, 23×23-57×57 were found by R. Gerbicz [7]. Many solutions also verified by Hannes Bassen.
References
[1] G. Hamilton. "Mondrian Art Puzzles." mathpickle. (Nov 23, 2016) mathpickle.com/project/mondrian-art-puzzles.
[2] E. Pegg Jr. "Blanche Dissections." Wolfram Community. (Nov 23, 2016) community.wolfram.com/groups/-/m/t/903043.
[3] "Tiling a Square with Rectangles." MathOverflow. (Nov 23, 2016) mathoverflow.net/questions/220567/tiling-a-square-with-rectangles.
[4] B. Haran. "Mondrian Art Puzzle." bradyharanblog.com. (Nov 23, 2016) www.bradyharanblog.com/blog/mondrian-art-puzzle.
[5] Numberphile (2016). Mondrian Puzzle—Numberphile" [video]. Retrieved November 23, 2016, from www.youtube.com/watch?v=49KvZrioFB0.
[6] "Mondrian Art Problem Upper Bound for defect." MathOverflow. (Dec 8, 2016) math.stackexchange.com/questions/2041189/mondrian-art-problem-upper-bound-for-defect.
[7] Mondrian Art Puzzles, mersenneforum.org/showthread.php?t=21775.
[8] oeis.org/A276523.
[9] oeis.org/A278970.
Permanent Citation