First-Order Transfer Functions in Process Control

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
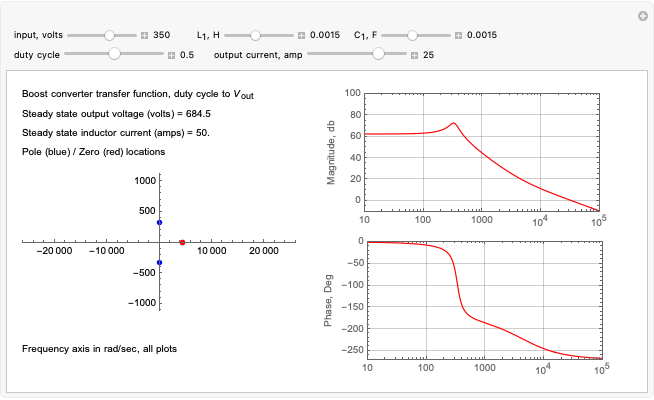
A transfer function is the ratio of the output to the input of a system. The system response is determined from the transfer function and the system input. A Laplace transform converts the input from the time domain to the spatial domain by using Laplace transform relations. The transformed spatial input is multiplied by the transfer function to get the output in the spatial domain. It is then converted back to the time domain using an inverse Laplace transform.
[more]
Contributed by: Simon M. Lane (May 2014)
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
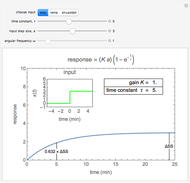
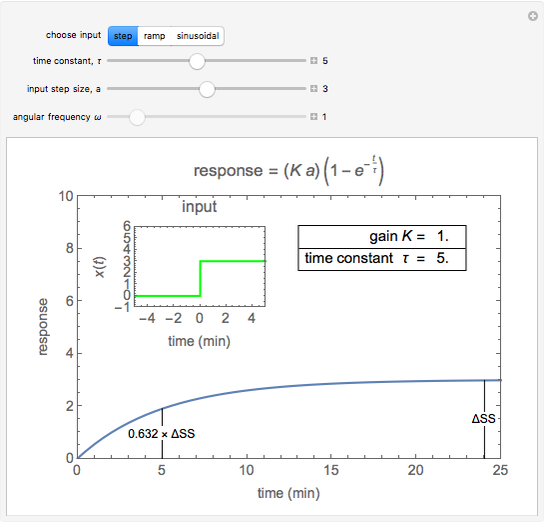
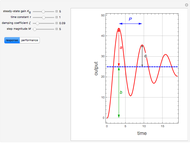
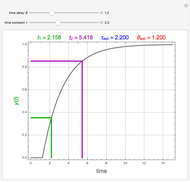
Step Input and Response
For a step input of magnitude  ,
,
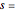 space domain
space domain
 time domain
time domain
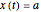
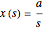
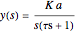

 time constant
time constant
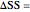 change in steady states
change in steady states
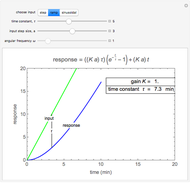
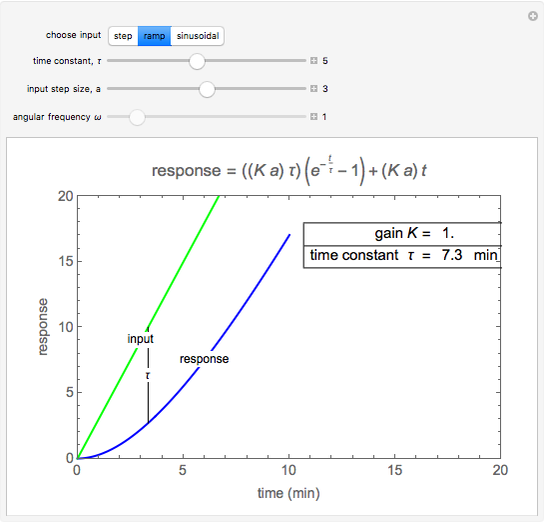
Ramp Input and Response
For a ramp input of magnitude  ,
,
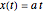
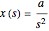
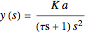
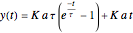
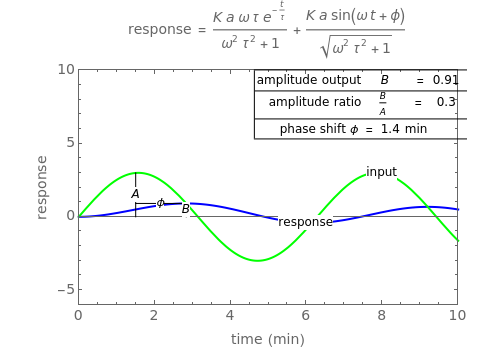
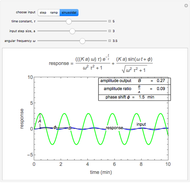
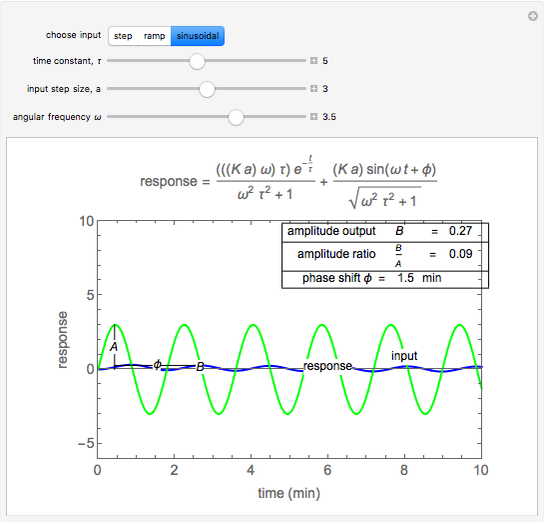
Sinusoidal Input and Response
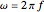 angular frequency, rate of change of the function
angular frequency, rate of change of the function
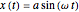
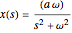
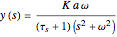
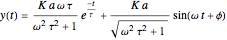
 phase shift, negative value represents a delay
phase shift, negative value represents a delay
time shift 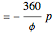
amplitude ratio 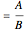
Permanent Citation