Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fermat's Theorem on Stationary Points

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Fermat's theorem on stationary points states that if is a local extremum in the interval 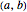and 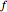is differentiable at , then .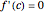

Contributed by: Julio Cesar de la Yncera (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

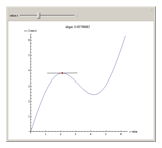
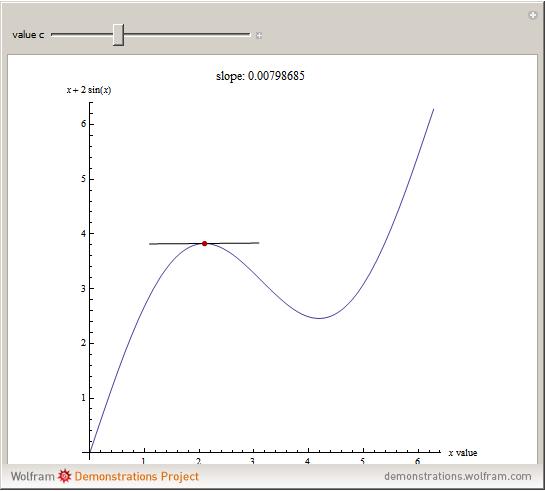
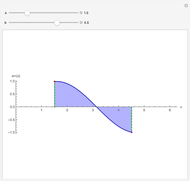
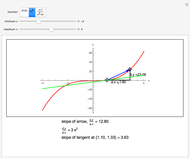
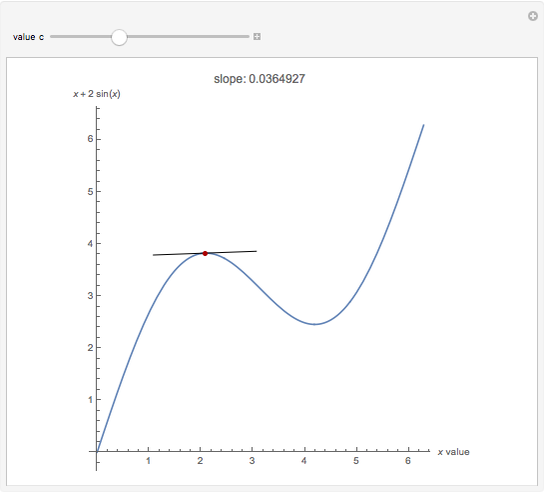
Snapshot 1: a local maximum; notice the slope is zero

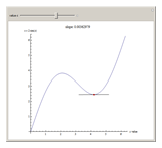
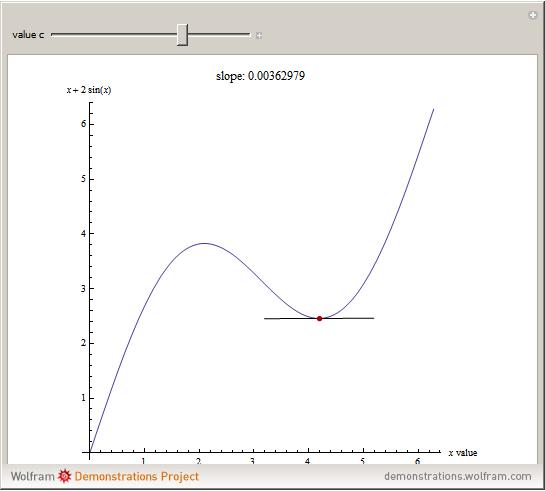
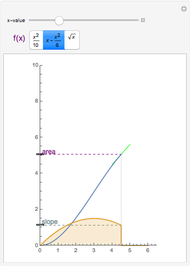
Snapshot 2: a local minimum; the slope is also zero here; also notice the change of sign from positive to negative for the maximum and from negative slope to positive slope for the minimum

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send