Forced Nonlinear Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
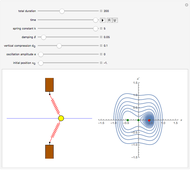
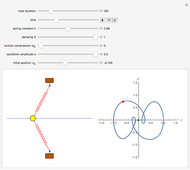
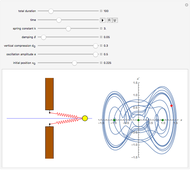
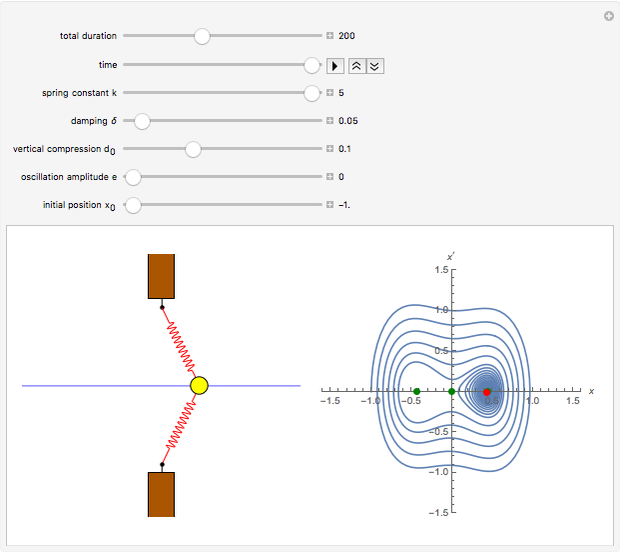
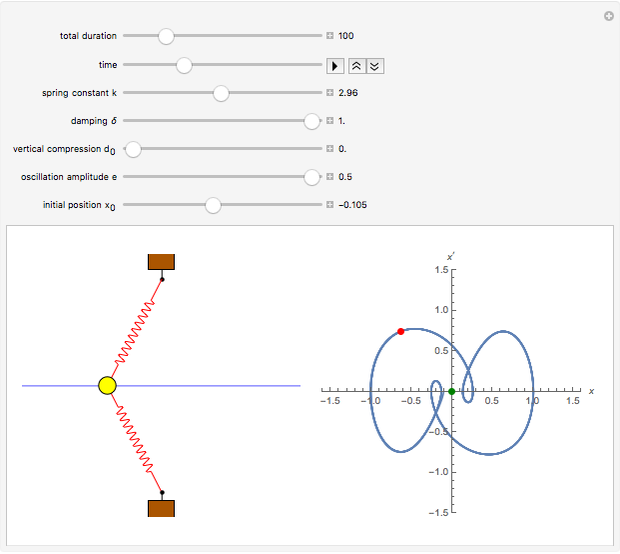
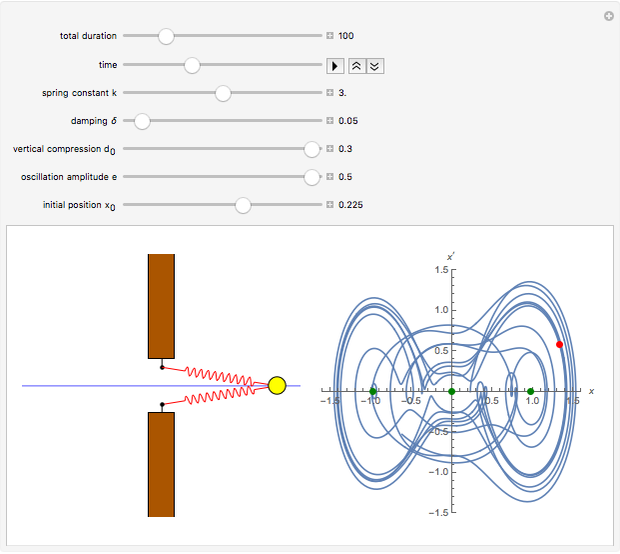
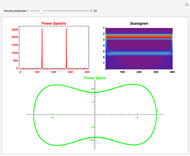
The oscillator consists of a unit mass, whose motion is restricted to a horizontal line, and two linear springs. The springs are attached to barriers, which are either fixed or oscillate in the vertical direction. The motion of the mass is governed by a nonlinear second-order differential equation, whose solution is calculated numerically. The phase plot shows the current position (red) and the equilibria (green), that is, points where the resultant force is zero.
Contributed by: Antonín Slavík (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let 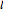 be the length of the unstretched spring,
be the length of the unstretched spring,  the spring constant,
the spring constant, 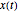 the position of the mass at time
the position of the mass at time  , and
, and 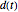 the distance of each barrier from the horizontal axis. The magnitude of the force exerted by each spring on the mass is
the distance of each barrier from the horizontal axis. The magnitude of the force exerted by each spring on the mass is  times the difference between the current and unforced lengths of the spring, that is,
times the difference between the current and unforced lengths of the spring, that is, 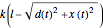 . The horizontal component of this force is
. The horizontal component of this force is 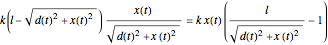 . This leads to the second-order differential equation
. This leads to the second-order differential equation 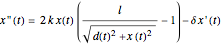 , where
, where 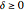 is the damping coefficient. The horizontal force is zero if
is the damping coefficient. The horizontal force is zero if 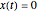 or
or 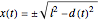 ; these are the coordinates at equilibrium.
; these are the coordinates at equilibrium.
Assume that 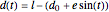 ; that is, the barriers are oscillating in the vertical direction. The values of the parameters
; that is, the barriers are oscillating in the vertical direction. The values of the parameters 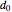 and
and  can be set by the "vertical compression" and "oscillation amplitude" sliders.
can be set by the "vertical compression" and "oscillation amplitude" sliders.
In the unforced case with 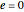 and
and 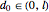 , the origin is an unstable equilibrium, and the remaining two equilibria are stable. A typical trajectory is periodic if
, the origin is an unstable equilibrium, and the remaining two equilibria are stable. A typical trajectory is periodic if 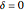 (no damping), or approaches one of the stable equilibria if
(no damping), or approaches one of the stable equilibria if 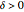 .
.
If  is nonzero, the differential equation becomes nonautonomous, and sufficiently large values of
is nonzero, the differential equation becomes nonautonomous, and sufficiently large values of  lead to unpredictable motion of the mass.
lead to unpredictable motion of the mass.
The situation is similar to the behavior of solutions to the Duffing equation [1, 2]. In fact, if  is a constant function (no forcing), and if we approximate the term
is a constant function (no forcing), and if we approximate the term 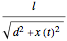 by its second-order Taylor expansion
by its second-order Taylor expansion 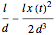 , we obtain the equation
, we obtain the equation 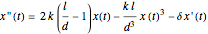 , which is a special case of the autonomous Duffing equation.
, which is a special case of the autonomous Duffing equation.
References
[1] I. Kovacic and M. J. Brennan (eds.), The Duffing Equation: Nonlinear Oscillators and Their Behaviour, Chichester, UK: John Wiley & Sons, 2011.
[2] A. Slavík, S. Wagon, and D. Schwalbe, VisualDSolve: Visualizing Differential Equations with Mathematica (2nd ed.), Champaign, IL: Wolfram Research, Inc., 2014.
Permanent Citation