The Damped Nonlinear Pendulum
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
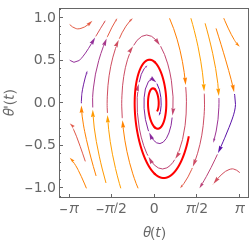
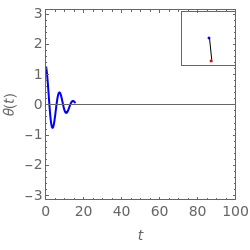
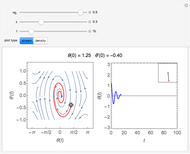
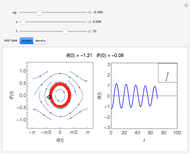
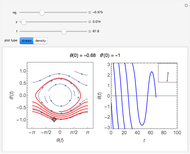
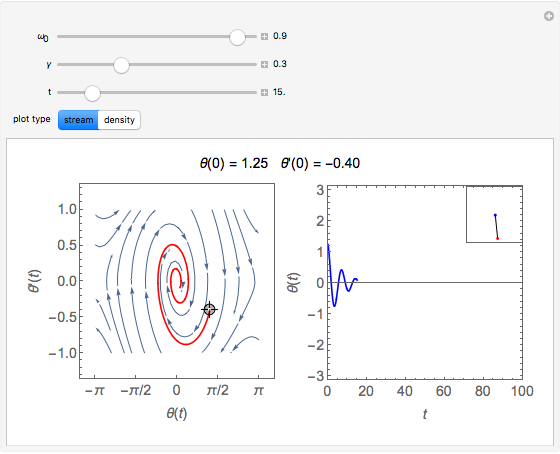
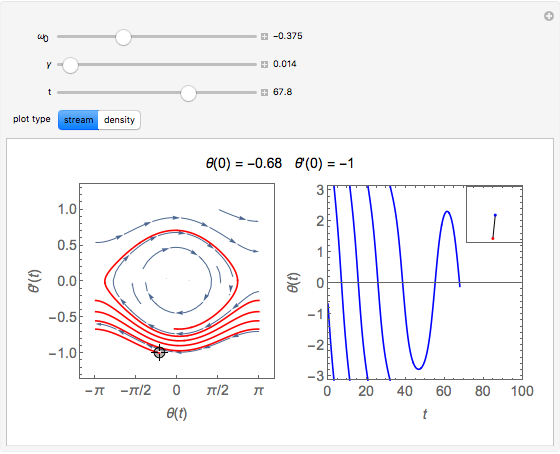
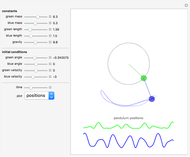
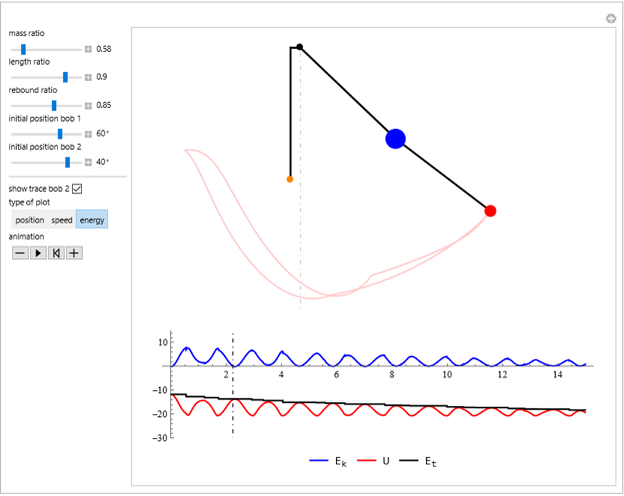
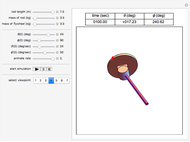
The plots show the motion of a harmonic oscillator with damping, in phase space on the left and as a function of time on the right, with the position of the pendulum in the top-right corner. The equation of motion is  , where
, where 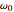 is the natural frequency and
is the natural frequency and  is the damping constant. This equation does not take the form of the usual approximation
is the damping constant. This equation does not take the form of the usual approximation 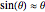 .
.
Contributed by: Enrique Zeleny (September 2018)
Open content licensed under CC BY-NC-SA
Details
Snapshots
Permanent Citation